神经网络中的数据表示

矩阵运算加块了神经网络的计算速度，而在应用中数据常常存储在多维Numpy数组中，其也被称为张量(tensor). 当前基本所有机器学习系统都使用张量作为数据结构，它对这个领域尤为的重要，以TensorFlow的命名就可窥见。

张量这一概念的核心在与，它是数据容器。 其中矩阵就是二维张量，张量事实上是矩阵向任意维度的推广。（张量的维度(dimension)常被称作轴(axis)，张量轴的个数被称为阶（rank））

标量（scalar）0D张量

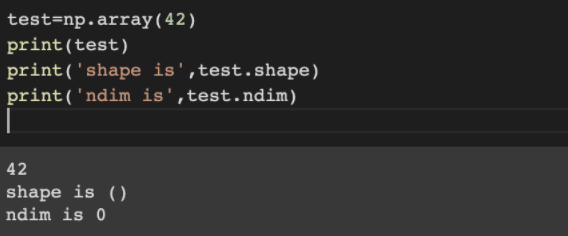
Numpy中，一个 float32和float64的数字就是一个0D张量。其可用ndim属性来查看。0D张量的ndim==0,如下图所示。

向量（vector）1D张量

很多数据中标签是存储在1D张量中的。其形式如下

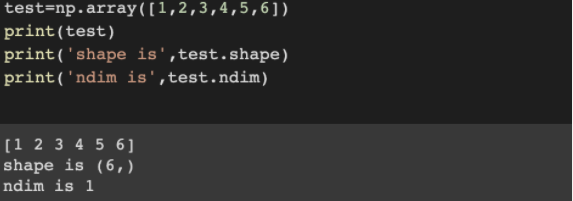
这个向量中有6个元素，被称为6D向量，易与张量的阶数混淆。事实上6D向量只有一个轴，沿着轴有6个维度(dimensionality)。6D张量才有6个轴。其中，维度既可以表示某个轴上的元素个数，也可以表示张量中的轴数。后者更准确的叫法应该是6阶张量。但是6D张量这种写法常见。

矩阵(matrix) 2D张量

向量组成的数组叫矩阵。矩阵有两个轴，通常称为行（row）和列(column)，其形式如下

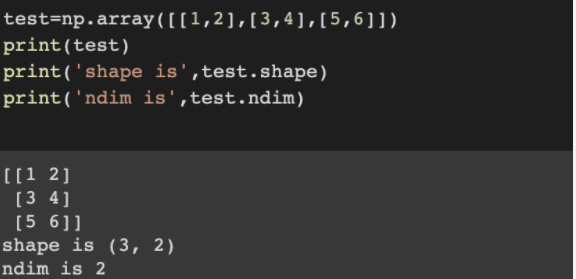
3X2的矩阵

3D张量

以CIFAR10数据集为例

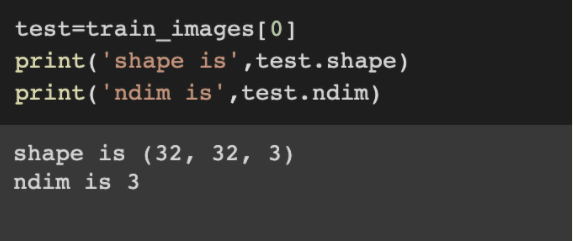
3D张量分别存储 高度 宽度和颜色深度，其大小为32*32像素，颜色深度维数为3，分别对应RGB三个颜色通道。

4D张量

关于4D张量：当许多图片累加起来时3D张量就不足以存储，需要增加一个拥有N维的轴来存储N个图片样本。

5D张量

关于5D张量：其中视频数据可以被看做事5D张量的少数数据类型之一，视频可以被看做由一系列帧（Frame）构成。每一个帧可以保存在一个形状为（height,width,color_depth）的3D向量中，一系列帧可以保存在(frames,height,width,color_depth)的4D张量中，不同视频数据组成的批量可以保存在5D张量中(samples,frames,height,width,color_depth)

神经网络中的数据表示

原文：https://www.cnblogs.com/echoml/p/14492484.html