[数据结构]并查集

概念：

并查集：是一种树型的数据结构，用于处理一些不相加集合的合并和查询问题。在使用中常常以森林来表示。 并查集也是用来维护集合的，和set得到不同之处在于并查集能很方便地同时维护很多集合。如果用set来维护会非常的麻烦。并查集的核心思想是记录每个结点的根结点是哪个结点。

主要函数组成：

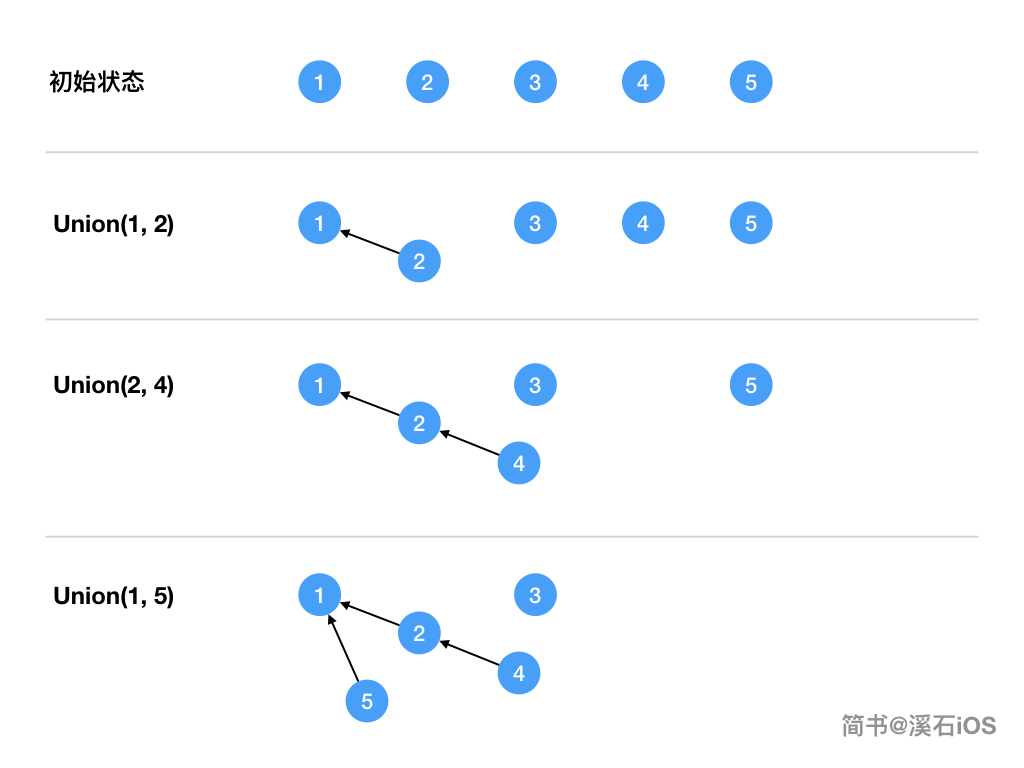
一个存储所有元素的数组：fri[N]  （朋友）

初始化：本文中使用函数名为 void init[N]    //N根据题目所包含元素个数决定。

此时所有的元素分别独立，fir[i]=i，都指向自己。

void init(int n)
{
    for (int i = 0;i < n;i++)
    {
        fri[i] = i;
    }
}

查找：本文中使用函数名为 int find(int x)

找x的朋友，一直到某个人的朋友为自己（根结点）为止。可用于判断两个人是否在同一个链上（假如在同一个链上，那么他们的根节点一定相同）

int find(int x)
{
    if (fri[x] == x)return x;//最终指向自己，退出递归
    return fri[x] = find(fri[x]);
}

合并/连接：本文中使用函数名为 int join(int x)

连接两个人（使两个人成为朋友），使fri[x]=y。

void join(int x, int y)
{
    x = find(x);
    y = find(y);
    if (x != y)//判断两人是否在同一条关系链。
    {
        fri[x] = y;
    }
}

总结：

1、用集合中的某个元素来代表这个集合，则该元素称为此集合的代表元；
2 、一个集合内的所有元素组织成以代表元为根的树形结构；
3 、对于每一个元素 x，fri[x] 存放 x 在树形结构中的朋友节点（如果 x 是根节点，则fri[x] = x）；
4 、对于查找操作，假设需要确定 x 所在的的集合，也就是确定集合的代表元。可以沿着fri[x]不断在树形结构中向上移动，直到到达根节点。

练习：《1192：朋友》

题意：

在社交的过程中，通过朋友，也能认识新的朋友。在某个朋友关系图中，假定 A 和 B 是朋友，B 和 C 是朋友，那么 A 和 C 也会成为朋友。即，我们规定朋友的朋友也是朋友。现在，已知若干对朋友关系，询问某两个人是不是朋友。

输入格式：

第一行：三个整数 n,m,p(n≤5000,m≤5000,p≤5000)分别表示有n 个人，m 个朋友关系，询问p 对朋友关系。

接下来 m 行：每行两个数Ai,Bi1≤Ai,Bi≤N，表示Ai? 和 Bi具有朋友关系。

接下来 p 行：每行两个数，询问两人是否为朋友。

输出格式：

输出共 p 行，每行一个Yes或No。表示第i个询问的答案为是否朋友。

题目链接：http://xujcoj.com/Home/Problems/status/pro_id/1192

制作：BDT20040

问题列表《1192：朋友》#并查集

原文：https://www.cnblogs.com/liubaili/p/14495079.html