继续有符号与无符号混合运算

前面记录一篇，关于有符号与无符号的混合运算，会有一些意想不到的结果

那么，我们是否可以“负负得正”呢？

什么情况下是不行的？

首先，不要被绕晕。

这是前提: 所有的无符号与有符号运算，都是先转成无符号运算的。结果返回 无符号，

那么，理论结果如果本身就是正数的，那实际就应该是正常的

如果结果不是正数的，那么是负数的无符号形式（最高位=1，其他位取反）

为了验证效果，（就验证加/减/乘/除），写段代码试试：

    int a = -20;
    unsigned int b = 10;

    //保持原始结果
    cout << "a+b=" << a + b << endl;    //希望：-10
    cout << "a*b=" << a * b << endl;     //希望：-200
    cout << "a-b=" << a - b << endl;       //希望：-30
    cout << "a/b=" << a / b << endl;       //希望：-2

    cout << "-a-b=" << -a - b << endl;     //希望：10
    cout << "-b+a=" << -b + a << endl;   //希望：-30

    //对结果进行强转
    cout << "a+b=" << (int)(a + b) << endl;
    cout << "a*b=" << (int)(a * b) << endl;
    cout << "a-b=" << (int)(a - b) << endl;
    cout << "a/b=" << (int)(a / b) << endl;

    cout << "-a-b=" << (int)(-a - b) << endl;
    cout << "-b+a=" << (int)(-b + a) << endl;

实际情况呢？

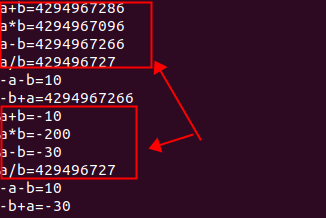
a+b是个无符号的结果，通过强转之后，是-10，可以负负得正，一般可控范围

a*b是个无符号的结果，通过强转之后，是-200，可以负负得正，一般可控范围

a-b是个无符号的结果，通过强转之后，是-30，可以负负得正，一般可控范围

a/b是个无符号的结果，通过强转之后，是429496727，不可以负负得正，属于不可控范围。

那么为什么只有除法不行了呢？

这个还是得从原理讲起，首先，乘法 跟 除法 都是通过移位来解决的

乘法是 左移

除法是 右移

然后，再看下，负数表达形式（以32位系统为例）。

-32 如果是无符号的话，是这样的：

如果是64bit，那么前面再多8个F

运算乘法 与 除法 之前，都先转 成 无符号的。

乘法，左移，之后，最高位仍然为1，当然前提数据不能溢出的情况，此时如果对结果再进行强转回来，至少符号位还是正常的

除法，右移，之后，最高位补0，那么就丢失了符号位，哪怕对结果再进行强转回来，也是由于缺少符号位，导致最后数据仍然不对！

-a - b，是个另类，-a的优先级，要高于 “减法” 运算符，因此，要先处理 -a 而不是先转成 无符号

           那也说得通：-a = 20， 无符号之后，仍然 20  ；20 - 10 = 10 ，没毛病

最后结论：

1. 如果没有除法的话，无符号跟有符号运算，可以仅对结果进行强转。（前提结果不能溢出）（不推荐这样做，推荐第2种做法）

2. 如果有除法，必须先给无符号转换成有符号的，再计算。

继续有符号与无符号混合运算

原文：https://www.cnblogs.com/winafa/p/14499949.html