将杂乱无章的数据元素,通过一定的方法按关键字顺序排列的过程叫做排序。
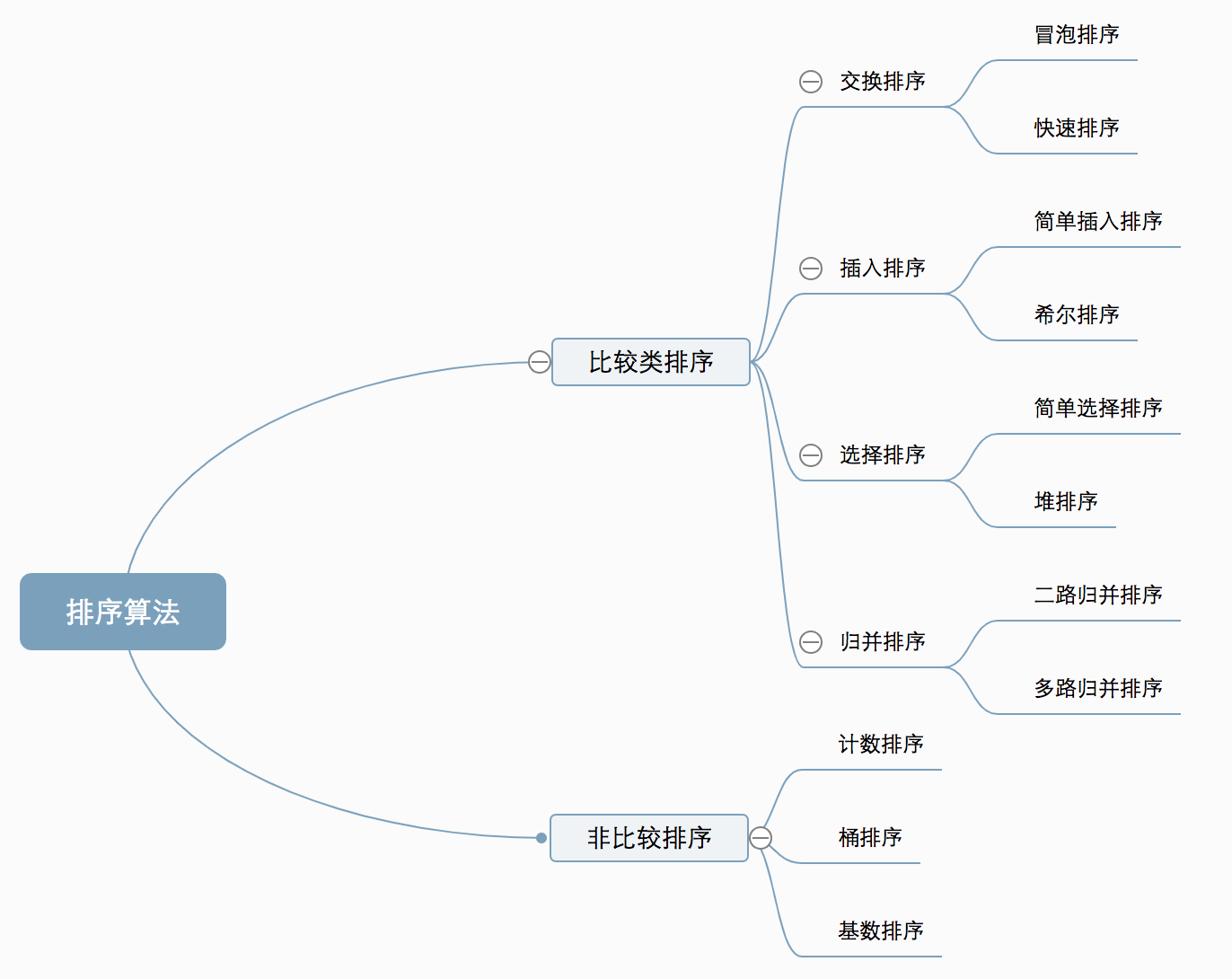
十种常见排序算法可以分为两大类:
非线性时间比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此称为非线性时间比较类排序。
线性时间非比较类排序:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此称为线性时间非比较类排序。
public class SortDemo { public static void main(String[] args) { int[] arr = {8, 4, 9, 2, 1, 6, 3, 7, 5, 8}; System.out.println("排序前:"); for (int i = 0; i < arr.length; i++) { System.out.print(arr[i] + " "); } System.out.println(""); System.out.println("排序后:"); sort1(arr); for (int i = 0; i < arr.length; i++) { System.out.print(arr[i] + " "); } } /*冒泡排序 * 依次比较相邻的两个元素,通过一次比较把未排序序列中最大(或最小)的元素放置在未排序序列的末尾 * */ public static void sort1(int[] arr) { System.out.println("冒泡排序:"); //外层循环,遍历次数 for (int i = 0; i < arr.length - 1; i++) { //内层循环,升序(如果前一个值比后一个值大,则交换) 第i趟比较arr.length-i次 //内层循环一次,获取一个最大值 for (int j = 0; j < arr.length - 1 - i; j++) { if (arr[j] > arr[j + 1]) { int temp = arr[j + 1]; arr[j + 1] = arr[j]; arr[j] = temp; } } } } }
1.4.1时间复杂度
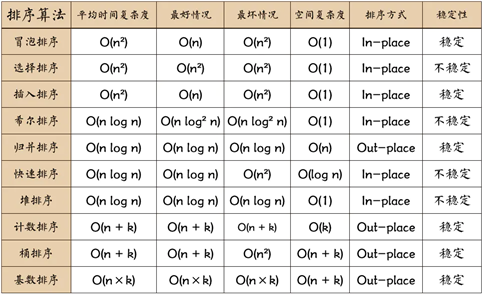
冒泡排序平均时间复杂度为O(n2),最好时间复杂度为O(n),最坏时间复杂度为O(n2)。
最好情况:如果待排序元素本来是正序的,那么一趟冒泡排序就可以完成排序工作,比较和移动元素的次数分别是 (n - 1) 和 0,因此最好情况的时间复杂度为O(n)。
最坏情况:如果待排序元素本来是逆序的,需要进行 (n - 1) 趟排序,所需比较和移动次数分别为 n * (n - 1) / 2和 3 * n * (n-1) / 2。因此最坏情况下的时间复杂度为O(n2)。
1.4.2 空间复杂度
冒泡排序使用了常数空间,空间复杂度为O(1)
1.4.3稳定性
当 array[j] == array[j+1] 的时候,我们不交换 array[i] 和 array[j],所以冒泡排序是稳定的。
1.4.4算法拓展
鸡尾酒排序,又称定向冒泡排序、搅拌排序等,是对冒泡排序的改进。在把最大的数往后面冒泡的同时,把最小的数也往前面冒泡,同时收缩无序区的左右边界,有序区在序列左右逐渐累积。
原文:https://www.cnblogs.com/loong-hon/p/14509988.html