leetcode 第 232 场周赛

第一次成功 \(AK\) \(leetcode\) 周赛，决定写篇博客记录一下。

这场周赛确实相对简单一些。

5701. 仅执行一次字符串交换能否使两个字符串相等

给你长度相等的两个字符串 s1 和 s2 。一次 字符串交换 操作的步骤如下：选出某个字符串中的两个下标（不必不同），并交换这两个下标所对应的字符。

如果对 其中一个字符串 执行 最多一次字符串交换 就可以使两个字符串相等，返回 true ；否则，返回 false 。

示例 1：

输入：s1 = "bank", s2 = "kanb"
输出：true
解释：例如，交换 s2 中的第一个和最后一个字符可以得到 "bank"

示例 2：

输入：s1 = "attack", s2 = "defend"
输出：false
解释：一次字符串交换无法使两个字符串相等

示例 3：

输入：s1 = "kelb", s2 = "kelb"
输出：true
解释：两个字符串已经相等，所以不需要进行字符串交换

示例 4：

输入：s1 = "abcd", s2 = "dcba"
输出：false

提示：

• 1 <= s1.length, s2.length <= 100
• s1.length == s2.length
• s1 和 s2 仅由小写英文字母组成

解决方案：

数据范围很小，暴力枚举所有可以交换的下标，时间复杂度 \(O(n^2)\) 。

class Solution {
public:
    bool areAlmostEqual(string s1, string s2) {
        int n = s1.size();
        for (int i = 0; i < n; ++i) {
            for (int j = i; j < n; ++j) {
                swap(s1[i],s1[j]);
                if (s1 == s2) return true;
                swap(s1[i],s1[j]);
            }
        }
        return false;
    }
};

5702. 找出星型图的中心节点

有一个无向的 星型 图，由 n 个编号从 1 到 n 的节点组成。星型图有一个 中心 节点，并且恰有 n - 1 条边将中心节点与其他每个节点连接起来。

给你一个二维整数数组 edges ，其中 edges[i] = [ui, vi] 表示在节点 ui 和 vi 之间存在一条边。请你找出并返回 edges 所表示星型图的中心节点。

示例 1：

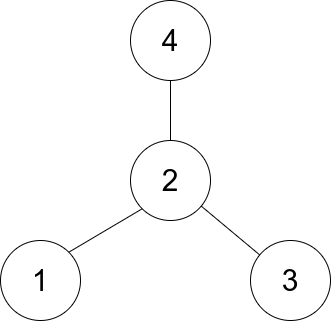
输入：edges = [[1,2],[2,3],[4,2]]
输出：2
解释：如上图所示，节点 2 与其他每个节点都相连，所以节点 2 是中心节点。

示例 2：

输入：edges = [[1,2],[5,1],[1,3],[1,4]]
输出：1

提示：

• 3 <= n <= 1e5
• edges.length == n - 1
• edges[i].length == 2
• 1 <= ui, vi <= n
• ui != vi
• 题目数据给出的 edges 表示一个有效的星型图

解决方案：

星型图的中心节点度为 \(n-1\) ，其余节点度为 \(1\) 。

随便找两条边，他们的公共顶点就是中心节点。

class Solution {
public:
    int findCenter(vector<vector<int>>& edges) {
        int a = edges[0][0], b = edges[0][1];
        if (edges[1][0] == a || edges[1][1] == a) return a;
        return b;
    }
};

5703. 最大平均通过率

一所学校里有一些班级，每个班级里有一些学生，现在每个班都会进行一场期末考试。给你一个二维数组 classes ，其中 classes[i] = [passi, totali] ，表示你提前知道了第 i 个班级总共有 totali 个学生，其中只有 passi 个学生可以通过考试。

给你一个整数 extraStudents ，表示额外有 extraStudents 个聪明的学生，他们 一定 能通过任何班级的期末考。你需要给这 extraStudents 个学生每人都安排一个班级，使得 所有 班级的 平均 通过率 最大 。

一个班级的 通过率 等于这个班级通过考试的学生人数除以这个班级的总人数。平均通过率 是所有班级的通过率之和除以班级数目。

请你返回在安排这 extraStudents 个学生去对应班级后的 最大 平均通过率。与标准答案误差范围在 10-5 以内的结果都会视为正确结果。

示例 1：

输入：classes = [[1,2],[3,5],[2,2]], extraStudents = 2
输出：0.78333
解释：你可以将额外的两个学生都安排到第一个班级，平均通过率为 (3/4 + 3/5 + 2/2) / 3 = 0.78333 。

示例 2：

输入：classes = [[2,4],[3,9],[4,5],[2,10]], extraStudents = 4
输出：0.53485

提示：

• 1 <= classes.length <= 1e5
• classes[i].length == 2
• 1 <= passi <= totali <= 1e5
• 1 <= extraStudents <= 1e5

解决方案：

给第 \(i\) 个班级新增一个聪明学生，其通过率的增量

出于贪心，每分配一个聪明学生，我们当然希望获得的增量尽可能大。

于是可以将每个班级放入优先队列，让队首元素的 \(\Delta_i\) 最大。不断为队首班级分配聪明学生即可。

时间复杂度 \(O((n+extraStudents)\cdot \log n)\) ，其中 \(n\) 代表 classes.length 。

struct node {
    int pass, tot;
    bool operator < (const node &t) const
    {
        double a = 1.0*(tot-pass)/tot/(tot+1);
        double b = 1.0*(t.tot-t.pass)/t.tot/(t.tot+1);
        return a < b;
    }
};
class Solution {
public:
    double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {
        priority_queue<node> Q;
        for (auto &cla : classes) {
            Q.push(node{cla[0],cla[1]});
        }
        
        // 不断为队首班级分配聪明学生
        while (extraStudents--) {
            node t = Q.top(); Q.pop();
            ++t.pass, ++t.tot;
            Q.push(t);
        }
        
        // 计算最终平均通过率
        double ans = 0;
        while (!Q.empty()) {
            node t = Q.top(); Q.pop();
            ans += 1.0*t.pass/t.tot;
        }
        ans /= classes.size();
        return ans;
    }
};

5704. 好子数组的最大分数

给你一个整数数组 nums （下标从 0 开始）和一个整数 k 。

一个子数组 (i, j) 的 分数 定义为 min(nums[i], nums[i+1], ..., nums[j]) * (j - i + 1) 。一个 好 子数组的两个端点下标需要满足 i <= k <= j 。

请你返回 好 子数组的最大可能 分数 。

示例 1：

输入：nums = [1,4,3,7,4,5], k = 3
输出：15
解释：最优子数组的左右端点下标是 (1, 5) ，分数为 min(4,3,7,4,5) * (5-1+1) = 3 * 5 = 15 。

示例 2：

输入：nums = [5,5,4,5,4,1,1,1], k = 0
输出：20
解释：最优子数组的左右端点下标是 (0, 4) ，分数为 min(5,5,4,5,4) * (4-0+1) = 4 * 5 = 20 。

提示：

• 1 <= nums.length <= 1e5
• 1 <= nums[i] <= 2e4
• 0 <= k < nums.length

解决方案：

首先用线段树或者 \(RMQ\) 可快速查询区间最小值。

注意到

• 当左端点不动时，右端点越靠右，区间最小值越小。
• 当右端点不动时，左端点越靠左，区间最小值越小。

于是不妨

• 遍历左端点 \(i\) ，找到一个最大的右端点 \(j\) ，使得 \(i,j\) 之间的最小值等于 \(i,k\) 之间的最小值，然后更新 ans 。
• 遍历右端点 \(j\) ，找到一个最小的左端点 \(i\) ，使得 \(i,j\) 之间的最小值等于 \(k,j\) 之间的最小值，然后更新 ans 。
• 上述最大右端点和最小左端点可通过二分法快速求得。

class RMQ
{
    vector<vector<int>> dpmi;
public:
    RMQ(vector<int> &nums) : dpmi(nums.size(), vector<int>(32))
    {
        int n = nums.size();
        for (int i = 0; i < n; ++i) dpmi[i][0] = nums[i];
        for (int j = 1, k = 2; k <= n; ++j, k <<= 1) {
            for (int i = 0; i+k-1 < n; ++i) {
                dpmi[i][j] = min(dpmi[i][j-1], dpmi[i+k/2][j-1]);
            }
        }
    }
    int qmin(int L, int R)
    {
        int j = log2(R-L+1), k = 1<<j;
        return min(dpmi[L][j], dpmi[R-k+1][j]);
    }
};

class Solution {
public:
    int maximumScore(vector<int>& nums, int k) {
        RMQ rmq(nums);
        int ans = 0;
        for (int i = 0; i <= k; ++i) {
            int val = rmq.qmin(i,k);
            int L = k, R = nums.size()-1;
            while (L < R) {
                int m = (L+R+1) >> 1;
                if (rmq.qmin(k, m) >= val) L = m;
                else R = m-1;
            }
            ans = max(ans, val*(L-i+1));
        }
        for (int j = k; j < nums.size(); ++j) {
            int val = rmq.qmin(k,j);
            int L = 0, R = k;
            while (L < R) {
                int m = (L+R) >> 1;
                if (rmq.qmin(m, k) >= val) R = m;
                else L = m+1;
            }
            ans = max(ans, val*(j-L+1));
        }
        return ans;
    }
};

leetcode 第 232 场周赛

原文：https://www.cnblogs.com/zbhfz/p/14531988.html