图像处理-余弦变换

什么是DCT？

DCT，Discrete Cosine Transform，DCT变换就是DFT变换的一种特殊形式，而其特殊点就在于其原始变换信号是一个实偶函数

它基于DFT，但只能使用实数，离散余弦变换相当于一个长度大概是它两倍的离散傅里叶变换，这个离散傅里叶变换是对一个实偶函数进行的（因为一个实偶函数的傅里叶变换仍然是一个实偶函数）

如何理解上面的话？

在开始讲DCT变换之前，我们来看看DFT的变换公式

当然，我们可以将上式子拆开来

显而易见的DFT变换的结果，实数部分由  承包了，而虚数部分则由  负责，设  ,那么，上式我们可以这样总结

实数部分：

虚数系数部分

显然的,cos是一个偶函数，sin是一个奇函数，因此有

因此，当  是一个实数函数时，其频域的实部是偶函数，虚部是一个奇函数。

那么，假如原信号  是一个全是实数的偶函数信号会怎么样，那么显然的，因为偶函数乘以偶函数还是偶函数，奇函数乘以偶函数还是奇函数，因此 就变成一个奇函数了，既然是奇函数那么自然

你看，一变换后虚部不见了，因此，当原时域信号是一个实偶信号时，我们就可以把DFT写成

其实上式就是DCT变换的核心思想了，但常见的DCT变换公式不一样

一维离散余弦变换

正变换：

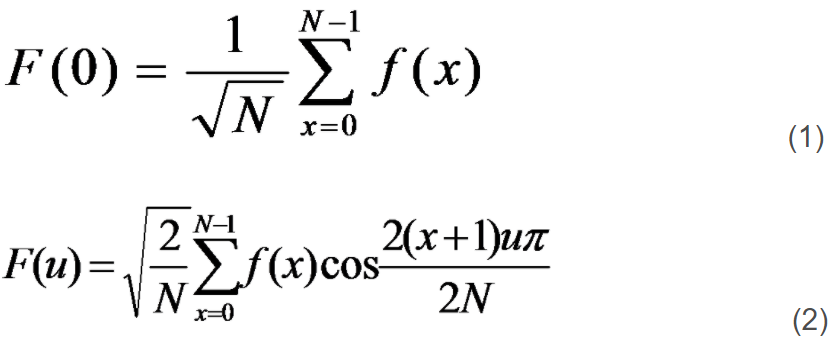
式中F(u)是第u个余弦变换系数，u是广义频率变量,u=1,2,3......N-1; f(x)是时域N点序列, x=0,1,2......N-1

反变换：

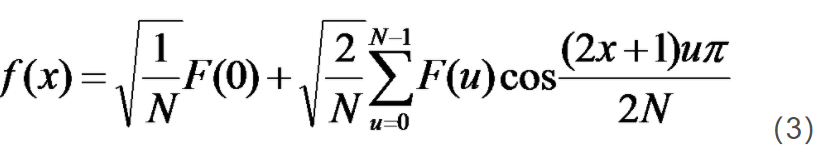
 显然，式(1)式(2)和式(3)构成了一维离散余弦变换对

二维离散余弦变换

正变换：

式(4)是正变换公式。其中f(x,y)是空间域二维向量之元素， x,y=0,1,2,......N-1；F(u,v)是变换系数阵列之元素。式中表示的阵列为N×N

反变换：

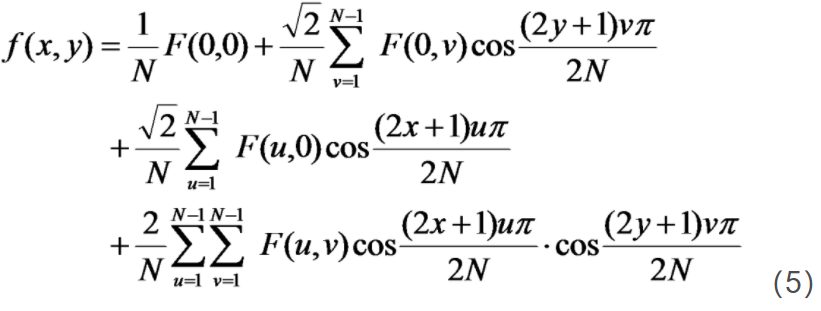
式中的符号意义同正变换式一样。式(4)和式(5)是离散余弦变换的解析式定义。

DCT变换公式

其中当u=0时否则

首先我们仍然明确一点，DCT变换就是DFT变换的一种特殊形式，这点没错，而其特殊点就在于其原始变换信号是一个实偶函数，但是实际应用中哪有那么多刚刚好的实偶函数信号给我们，因此为了适用面更广，既然自然界没有那么多实偶信号，我们就用实信号造一个。

设一长度为N的实数离散信号  ,首先,我们先将这个信号长度扩大成原来的两倍,并变成2N,定义新信号  为

简单来说,这个信号变成了如图(1.0)所示的样子

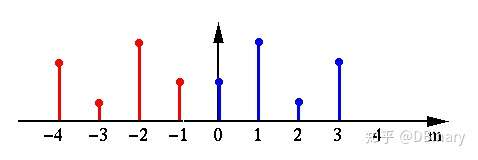
其中，蓝色为原始信号，红色为延拓后的信号这样，我们就将一个实信号变成了一个实偶信号，那么，对这个延拓的信号的DFT变换怎么写呢，显然，信号的区间已经从之前的  变成了  ,因此，DFT变换公式也变成了

但是，这样的插值之后也随之带来了一个问题，这个信号并不关于m=0偶对称，它关于  对称，因此，为了让信号仍然关于原点对称，把整个延拓的信号向右平移  个单位是个不错的主意

为此，式1.3也得做出对应的改变

依据欧拉公式对式1.4进行展开，展开时我们只要实数部分就行了，因为之前讨论过了，虚数部分已经是0了

到这一步显然还不够科学，毕竟m算出来居然是一个小数还带负数，作为一个离散序列我去哪找这个值，因此，式1.5我们还需要进一步变形，首先我们知道，这个序列是一个偶对称序列，因此根据式1.5

然后，设  ，并将n代入到式1.6中

好了，我们距离常用DCT的标准式已经非常的接近了，现在问题就是那个标准式里的那个  是个啥玩意。

实际上这个  如果在函数计算中，加不加都无所谓，实际上在DFT变换中，这个值也是存在的因为常常取1，因此没有再进一步写出来，实际上，这个值因为一些工程学上的意义，DFT中也常常会取  或 

那么，DCT中它的出现，主要是为了在DCT变换变成矩阵运算的形式时，将该矩阵正交化以便于进一步的计算，那么，这个系数就应该取  

将这个系数乘到式1.7中，即可得到DCT变换公式

矩阵表示法

更为简洁的定义方法是采用矩阵式定义。根据以上公式定义可知，离散余弦变换的系数矩阵可以写成如下：

 如果令N＝4，那么由一维解析式定义可得如下展开式。

写成矩阵式

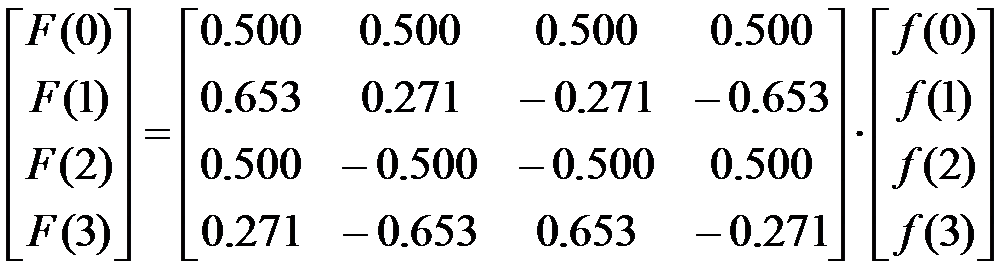
若定义F(u)为变换矩阵，A为变换系数矩阵，f(x)为时域数据矩阵，则一维离散余弦变换的矩阵定义式可写成如下形式

同理，可得到反变换展开式

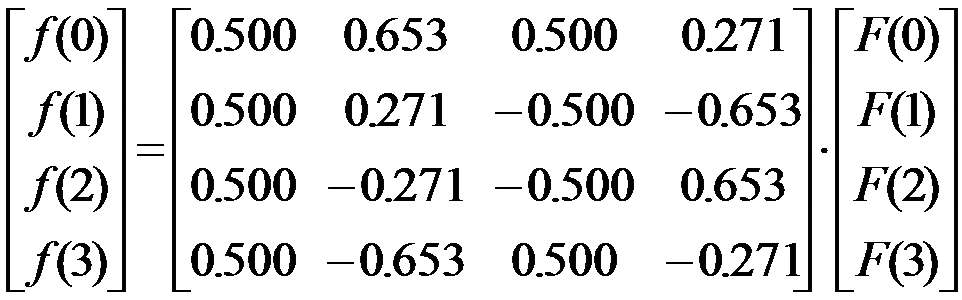
写成矩阵式即：

二维离散余弦变换也可以写成矩阵式：

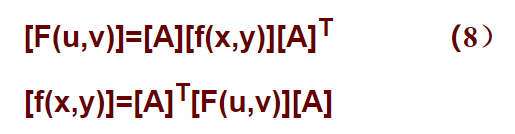
式中[f(x,y)]是空间数据阵列，A是变换系数阵列，[F(u,v)]是变换矩阵，[A]T是[A]的转置

对二维图像进行离散余弦变换

由以上对二维离散余弦变换的定义及公式（7）可知，求二维图像的离散余弦变换要进行以下步骤：

• 1.获得图像的二维数据矩阵f(x,y)；
• 2.求离散余弦变换的系数矩阵[A]；
• 3.求系数矩阵对应的转置矩阵[A]T；
• 4.根据公式（7）[F(u,v)]=[A][f(x,y)][A]T 计算离散余弦变换；

优点

1、DCT变换较DFT变换具有更好的频域能量聚集度（说人话就是能够把图像更重要的信息聚集在一块），那么对于那些不重要的频域区域和系数就能够直接裁剪掉（有点像淘金，你把石头里重要的金子都弄到一块，剩下没啥用的石子不就可以扔了么），因此，DCT变换非常适合于图像压缩算法的处理，例如现在大名鼎鼎的jpeg就是使用了DCT作为图像压缩算法

2、DCT变换是可分离的变换，其变换核为余弦函数。DCT除了具有一般的正交变换性质外， 它的变换阵的基向量能很好地描述人类语音信号和图像信号的相关特征。因此，在对语音信号、图像信号的变换中，DCT变换被认为是一种准最佳变换。

二维DFT与二维DCT的频谱特征分析

1、细节（高频分量）较少的图像实验：

Conclusion：
对于比较平滑的图像/数据，DFT变换数据集中在中间（低频信号区），DCT变换数据集中在左上角，几乎无法看出DCT的优势在哪里。
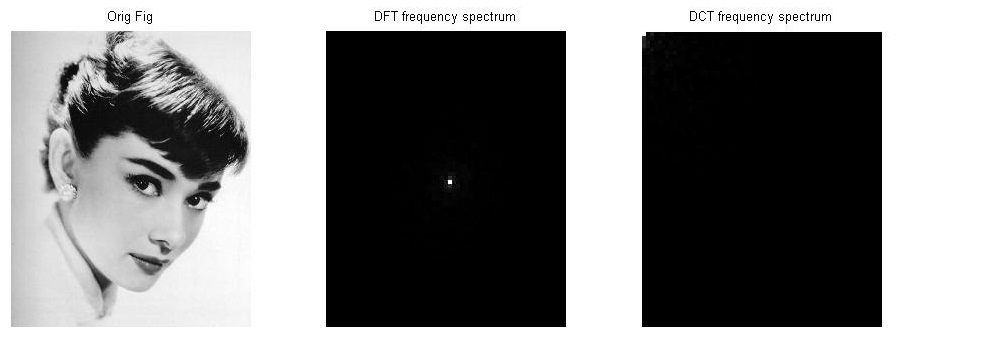
2、细节丰富的图像实验

Conclusion：
DCT变化后的数据很发散，DCT变化后的数据仍然比较集中。如果同样从频率谱恢复原始图像，那么选用DCT更合理，因为DCT只需要存储更少的数据点。正是这个原因，是的DCT广泛地应用于图像压缩。

应用

DCT应用于图像压缩

16*16 进行分区做DCT变换，然后按照不同的模板进行数据存留与重建。我们会发现，如果保存的数据过少，会有块效应现象发生。

64*64的分区设置，块效应更明显。此时就要在每个分区内多采集点数据。

DCT在JPEG压缩编码中的应用

JPEG(Joint Photographic Experts Group) 专家组开发了两种基本的压缩算法，一种是采用以离散余弦变换(DCT)为基础的有损压缩算法，另一种是采用以预测技术为基础的无损压缩算法。使用有损压缩算法时，在压缩比为25:1的情况下，压缩后还原得到的图像与原始图像相比较，非图像专家难于找出它们之间的区别，因此得到了广泛的应用。

JPEG算法的主要计算步骤：

• 正向离散余弦变换(FDCT)
• 量化(quantization)
• Z字形编码(zigzag scan)
• 使用差分脉冲编码调制(differential pulse code modulation，DPCM)对直流系数(DC)进行编码 
• 使用行程长度编码(run-length encoding，RLE)对交流系数(AC)进行编码
• 熵编码(entropy coding）

DCT在数字水印中的应用

水印检测框图：

实验

matlab基础

DCT变换

%读入测试图像 
mypicture=imread(‘input.jpg‘);%显示读入的图像 %为了防止后一个显示的图像覆盖前一个显示结果，每次显示时调用figure生成一个新窗口 	
figure(),imshow(mypicture),title(‘原输入图像‘);

 　　　　　　　　　　　　图一

转为灰度图：

grayImage=rgb2gray(mypicture);%如果读入的是彩色图像则转化为灰度图像（灰度图像省略这一步） 
figure(),imshow(grayImage),title(‘原输入彩色图像转化为灰度图像‘); 

 　　　　　　　　　　　　图二

对图像DCT转换：

%对图像DCT变换  
dctgrayImage=dct2(grayImage);
figure(), imshow(log(abs(dctgrayImage)),[]),title(‘DCT变换灰度图像‘), colormap(gray(4)), colorbar;

 　　　　　　　　　图三

对灰度矩阵进行量化：

%对灰度矩阵进行量化
dctgrayImage(abs(dctgrayImage)<0.1)=0; 

DCT逆变换：

%DCT逆变换  
I=idct2(dctgrayImage)/255;  
figure(), imshow(I), title(‘经过DCT变换，然后逆变换的灰度图像‘);

 　　　　　　　　　　　　图四

对比变换傅里叶变换前后的图像 ：

%对比变换傅里叶变换前后的图像  
figure(), subplot(121), imshow(grayImage), title(‘原灰度图像‘), 
subplot(122), imshow(I), title(‘DCT逆变换图像‘);

 　　　　　　　　　　　　　　　图五

结果分析：对原始图像进行离散余弦变换，如图3所示，由结果可知，变换后DCT系数能量主要集中在左上角，其余大部分系数接近于零，这说明DCT具有适用于图像压缩的特性。将变换后的DCT系数进行门限操作，将小于一定值得系数归零，这就是图像压缩中的量化过程，然后进行逆DCT运算，得到压缩后的图像，如图4。由图5比较变换前后的图像，肉眼很难分辨出有什么区别，可见压缩的效果比较理想

参考

1、百度百科

2、知乎

3、DCT实现图像压缩

4、CSDN1   CSDN2 

5、Matlab实现

图像处理-余弦变换

原文：https://www.cnblogs.com/pam-sh/p/14533603.html