
题意:给两个数N与X,其中N 为数组中数的个数,数组中的每一个数除以X并向上取整,此外,数组中的数可以与其周围的数合并(即相加)求结果的最小值与最大值
思路:由于向下取证的原因,不断的合并只会让结果变小,所以最小值为一直合并的结果,最大值为不合并的结果
#include<iostream> #define rep(i,n) for(i=1;i<=n;++i) using namespace std; typedef long long ll; int main() { ll t, n, x, ans, sum, i, temp, mi; cin >> t; while (t--) { ans = 0; sum = 0; cin >> n >> x; rep(i, n) { cin >> temp; int k = temp % x; if (k)ans = ans + temp / x + 1; else ans += temp / x; sum += temp; } if (sum % x == 0)mi = sum / x; else mi = sum / x + 1; cout << mi <<" "<< ans << endl; } }
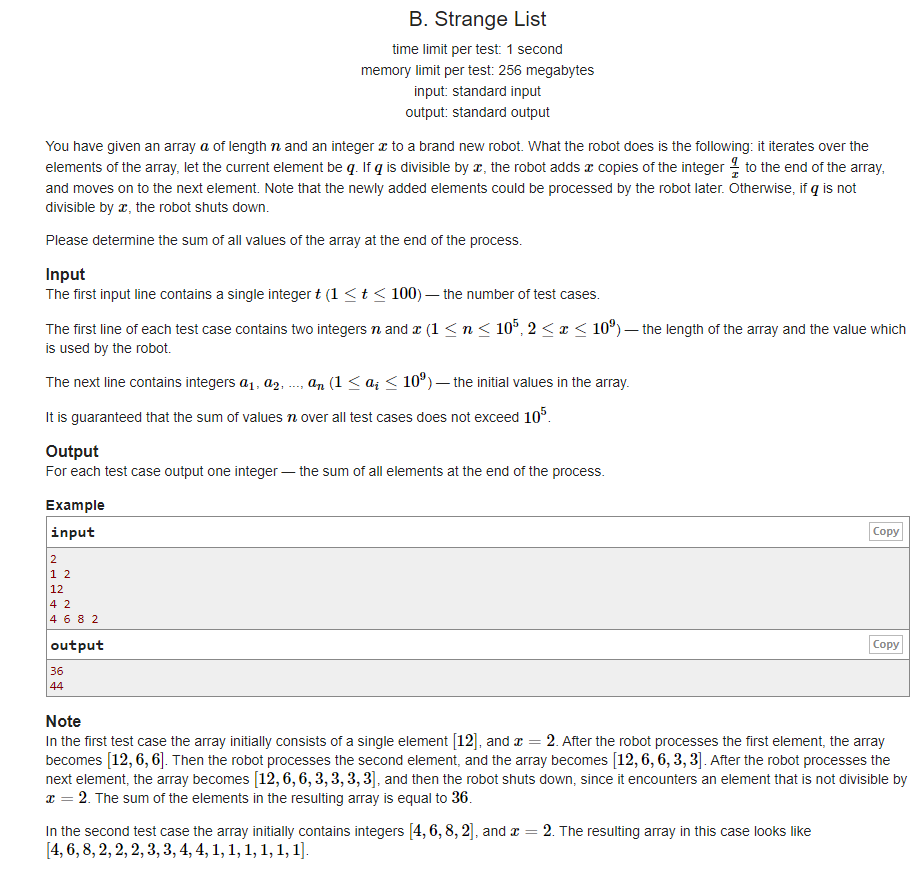
题意:累了,不想翻译
思路:我们可以对数组的每个数都不断的除于X,得到其最小的层数(可以被a[I]除的次数),对于取得最小的层数所在的数之前的每个数*(层级+1),之后则是*层数;同时用一个前缀和数组加快运算
#include<iostream> #include<cstring> #define rep(i,n) for(i=1;i<=n;++i) #define ms(a,n) memset(a,n,sizeof(a)) #define maxn 100005+5 #define inf 0x3f3f33f3f using namespace std; typedef long long ll; ll t, n, x, ans, sum[maxn], i, temp, mi, rank_m, rank_n; int main() { cin >> t; while (t--) { ms(sum, 0); rank_m = inf; cin >> n >> x; rep(i, n) { cin >> temp; sum[i] = temp + sum[i - 1]; int f = temp; rank_n = 1; while (f % x==0) { rank_n++; f /= x; } if (rank_n < rank_m) { rank_m = rank_n; mi = i; } } ans = (rank_m + 1) * sum[mi-1] + (sum[n] - sum[mi-1]) * rank_m; cout << ans << endl; } }
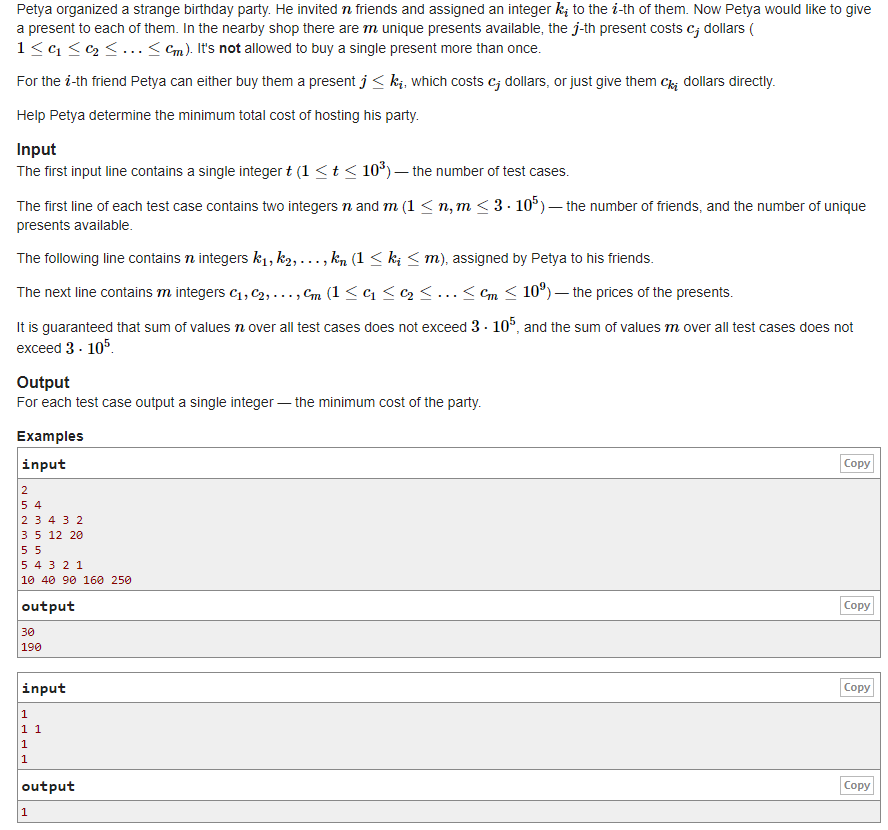
题意:同上
思路:贪心。
#include<iostream> #include<cstring> #include<algorithm> #define rep(i,n) for(i=1;i<=n;++i) #define ms(a,n) memset(a,n,sizeof(a)) #define maxn 100005+5 #define inf 0x3f3f33f3f using namespace std; typedef long long ll; ll t, n, x, ans, i, temp, k[maxn], sz[maxn], m, cnt; bool mc(ll a, ll b) { return a > b; } int main() { cin >> t; while (t--) { cin >> n >> m; rep(i, n)cin >> k[i]; rep(i, m)cin >> sz[i]; sort(k + 1, k + n + 1, mc); cnt = 1; ans = 0; rep(i, n) { if (k[i] <= cnt) ans += sz[k[i]]; else ans += sz[cnt++]; } cout << ans << endl; } }
Codeforces Round #694 (Div. 2) A B C题解
原文:https://www.cnblogs.com/ggnpgl/p/14540062.html