你有一个长度为 \(n(n\le200000)\) 的序列,每个数的权值小于 \(2^m(m\le53)\)。 定义一个子序列的权值为子序列所有数的异或和的二进制表示中 \(1\) 的个数。 对于所有 \(i\in[0,m]\),输出所有 \(2^n\) 个子序列中权值为 \(i\) 的子序列的个数 \(\bmod 998244353\) 的值。
看了一晚上的神仙题,来复读一下题解。
?
首先 ,定义 \(\mathrm{popcount}(s)\) 表示 \(s\) 二进制表示中 \(1\) 的个数,\((i,j)\) 表示 \(\mathrm{popcount}(i\&j)\),\(\mathrm{span}(S)\) 表示 \(S\) 张成的向量空间,\(F(S)\) 表示 \(\mathrm{span}(S)\) 对应的集合幂级数 \(\sum\limits_{i\in \mathrm{span}(S)}z^i\),\(G(S)\) 表示 \(F(S)\) 的关于 \(\mathrm{popcount}\) 的占位多项式 \(\sum\limits_{i\in \mathrm{span}(S)}z^{\mathrm{popcount}(i)}\),\(|S|\) 表示集合 \(S\) 的大笑,\(U\) 是给定的数的集合,\(A\) 是给定的数的一组基。
?
结论 1:\(\forall i\in \mathrm{span}(U)\),其被生成的方案数均为 \(2^{|U|-|A|}\),因为对于任意不在 \(A\) 中的元素,无论怎么选都有唯一确定的一种选择 \(A\) 中元素的方案使得结果最后为 \(i\)。于是我们现在只需要考虑 \(A\) 中的元素,最后把答案乘上 \(2^{|U|-|A|}\) 即可。
?
我们考虑按 \(|A|\) 进行分治,如果 \(|A|<\dfrac{m}{2}\),那么我们暴力枚举 \(A\) 中每个数的选取情况,这样我们得到了一个 \(O(2^{|A|})\) 的算法。
如果 \(|A|\geqslant \dfrac{m}{2}\),下面给出一个 \(O(2^{m-|A|})\) 的算法,这样我们分治即可做到 \(O(2^{\frac{m}{2}})\) 的复杂度。
?
结论 2:注意到由于 \(\mathrm{span}(A)\) 内部元素任意异或后的结果还在 \(\mathrm{span}(A)\) 中,于是我们有
枚举所有属于 \(\mathrm{span}(A)\) 的元素,故有
其中 \(*\) 是异或卷积,\(\cdot\) 是按位乘。注意到方程 \(x^2=2^{|A|}x\) 的解只有 \(x=0/x=2^{|A|}\),所以 \(FWT(F(A))\) 中的每一个元素只可能是 \(0\) 或 \(2^{|A|}\)。
?
结论 3:考虑 FWT 的定义式
注意到 \([z^j]F(A)\) 有值的位置只有 \(2^{|A|}\) 种,所以当且仅当 \(\forall j\in \mathrm{span}(A)\),\(2\mid (i,j)\),才有 \([z^i]FWT(F(A))=2^{|A|}\),其他情况为 \(0\)。同时注意到 \((i,x)\oplus (j,x)=(i\oplus j,x)\),所以可以把上面条件中的 \(\mathrm{span}(A)\) 改为 \(A\)。
?
结论 4:存在一组基 \(B\),使得 \(\forall x\in \mathrm{span}(A),y\in \mathrm{span}(B)\),\(2\mid (x,y)\),且 \(|A|+|B|=m\)。
我们考虑一个构造,把 \(A\) 中的元素消元(即每个主元只在一个数中出现),然后构造一个矩阵,第 \(i\) 行是主元为 \(i\) 的数,如果 \(A\) 中不含以某个数为主元的数,就把这一行除了主元填 \(1\),其他填 \(0\),这样会形成一个上三角矩阵,再把这个矩阵沿主对角线对称,之前没有的主元的行构成了 \(B\)。如图(来自官方题解):
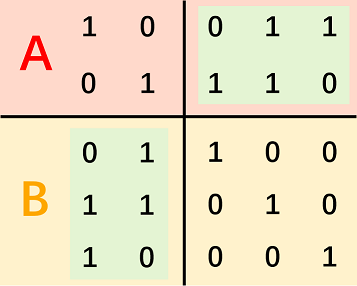
根据结论 3,我们也只需要考虑 \(A,B\) 中的任意两个元素 \(x,y\),注意到如果 \(y\) 的主元在 \(x\) 对应的位置是 \(1\),那么 \(x\) 的主元在 \(y\) 对应的位置也是 \(1\),而其他位置都是 \(0\)(因为消过了元),所以 \((x,y)=0/2\)。
根据上面的定义与结论 3,有以下结论:
?
现在我们考虑计算答案,注意到
其中 \(G_c=\sum\limits_{\mathrm{popcount}(i)=c}z^i\)。
那么 \([z^i]P(A)=[z^0](F(A)*G_c)=[z^0]IFWT(FWT(F(A))\cdot FWT(G_c))\),注意到 \(IFWT(F)=2^{-m}[z^0]FWT(F)=\dfrac{1}{2^m}\sum [z^i]F\),于是:
?
结论 5:\([z^i]FWT(G_c)\) 的值只和 \(\mathrm{popcount}(i)\) 有关,因为每一位的“地位”都是相同的。
?
所以我们考虑同时把 \(B\) 和 \(FWT(G_c)\) 按 \(\mathrm{popcount}\) 分类,于是有
后面是按 FWT 的定义枚举 \((i,d)\)。
所以暴力求出 \(P(B)\),并按照式子计算即可。
所以我们可以在 \(O(nm+2^{\frac{m}{2}}+m^3)\) 的时间内解决此问题。
CF1336E2 Chiori and Doll Picking (hard version)
原文:https://www.cnblogs.com/AzusaCat/p/14584154.html