对于仍然不太清楚位操作符的同学们，可以看看这篇文章：位操作符

特别注意

特别注意：使用按位操作符时要注意，相等（==）与不相等（!=）的优先级在按位运算符之上！！！！
这意味着，位运算符的优先级极小，所以使用位运算符时，最好加上括号()

重要技巧

基本的操作我就直接略过了。下面是我认为必须掌握的技巧：（注意，我把一些生僻的技巧都已经砍掉了，留下来的，就是我认为应该会的）

1. 使用 x & 1 == 1 判断奇偶数。（注意，一些编辑器底层会把用%判断奇偶数的代码，自动优化成位运算）

2. 不使用第三个数，交换两个数。x = x ^ y ， y = x ^ y ， x = x ^ y。（早些年喜欢问到，现在如果谁再问，大家会觉得很low）

3. 两个相同的数异或的结果是 0，一个数和 0 异或的结果是它本身。（对于找数这块，异或往往有一些别样的用处。）

4. x & (x - 1) ，可以将最右边的 1 设置为 0。（这个技巧可以用来检测 2的幂，或者检测一个整数二进制中 1 的个数，又或者别人问你一个数变成另一个数其中改变了多少个bit位，统统都是它）

5. i+(~i)=-1，i 取反再与 i 相加，相当于把所有二进制位设为1，其十进制结果为-1。

6. 对于int32而言，使用 n >> 31取得 n 的正负号。并且可以通过 (n ^ (n >> 31)) - (n >> 31) 来得到绝对值。（n为正，n >> 31 的所有位等于0。若n为负数，n >> 31 的所有位等于1，其值等于-1）

7. 使用 (x ^ y) >= 0 来判断符号是否相同。（如果两个数都是正数,则二进制的第一位均为0,x^y=0；如果两个数都是负数,则二进制的第一位均为1；x^y=0 如果两个数符号相反,则二进制的第一位相反,x^y=1。有0的情况例外，^相同得0，不同得1）

8. “异或”是一个无进位加法，说白了就是把进位砍掉。比如01^01=00。

9. “与”可以用来获取进位，比如01&01=01，然后再把结果左移一位，就可以获取进位结果。

使用掩码遍历二进制位

这个方法比较直接。我们遍历数字的 32 位。如果某一位是 1 ，将计数器加一。

我们使用 位掩码 来检查数字的第 \(i^{th}\) 位。一开始，掩码 m=1 因为 1 的二进制表示是

\[0000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0001\]
0000 0000 0000 0000 0000 0000 0000 0001

显然，任何数字跟掩码 11 进行逻辑与运算，都可以让我们获得这个数字的最低位。检查下一位时，我们将掩码左移一位。

\[0000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0010\]
0000 0000 0000 0000 0000 0000 0000 0010

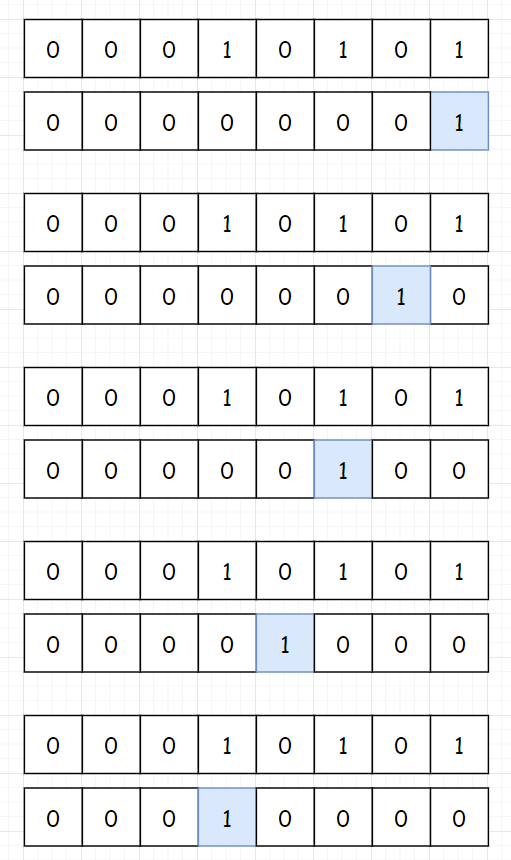
并重复此过程，我们便可依次遍历所有位。

Java

public int hammingWeight(int n) {
    int bits = 0; // 用来储存 1 的个数

    int mask = 1;  // 掩码，从最低位开始

    for (int i = 0; i < 32; i++) {
        // 注意这里是不等于0，而不是等于1，因为我们的位数是不断在变化的，可能等于2、4、8...
        // 使用按位操作符时要注意，相等（==）与不相等（!=）的优先级在按位运算符之上！！！！
        // 使用按位运算符时，最好加上括号()
        if ((n & mask) != 0) {
            bits++;
        }
        mask <<= 1;
    }
    return bits;
}

注意：这里判断 n & mask 的时候，千万不要错写成 (n & mask) == 1，因为这里你对比的是十进制数。（我之前就这么写过，记录一下...）

无符号右移遍历二进制位

逐位判断
根据 与运算 定义，设二进制数字 n ，则有：

• 若 \(n \& 1 = 0\)，则 n 二进制 最右一位 为 00 ；
• 若 \(n \& 1 = 1\)，则 n 二进制 最右一位 为 11 。

根据以上特点，考虑以下 循环判断 ：

1. 判断 n 最右一位是否为 1 ，根据结果计数。
2. 将 n 右移一位（本题要求把数字 n 看作无符号数，因此使用 无符号右移 操作）。

算法流程：

1. 初始化数量统计变量 res = 0。
2. 循环逐位判断： 当 n = 0 时跳出。
3. res += n & 1 ： 若 \(n \& 1 = 1\) ，则统计数 res 加一。
4. n >>= 1 ： 将二进制数字 n 无符号右移一位（ Java 中无符号右移为 ">>>" ） 。
5. 返回统计数量 res。

public class Solution {
    public int hammingWeight(int n) {
        int res = 0;
        while(n != 0) {
            res += n & 1;  // 遍历
            n >>>= 1;  // 无符号右移
        }
        return res;
    }
}

反转最后一个 1

对于特定的情况，如 只有 1 对我们有用时，我们不需要遍历每一位，我们可以把前面的算法进行优化。

我们不再检查数字的每一个位，而是不断把数字最后一个 1 反转，并把答案加一。当数字变成 0 的时候偶，我们就知道它没有 1 的位了，此时返回答案。

注意：这里我们说的是最后一个 1，而不是最后一位 1，这个 1 可能在任何位上。

这里关键的想法是对于任意数字 n ，将 n 和 n - 1 做与运算，会把最后一个 1 的位变成 0 。为什么？考虑 n 和 n - 1 的二进制表示。

巧用 \(n \& (n - 1)\)
\((n - 1)\) 解析： 二进制数字 n 最右边的 1 变成 0 ，此 1 右边的 0 都变成 1 。
\(n \& (n - 1)\) 解析： 二进制数字 n 最右边的 1 变成 0 ，其余不变。

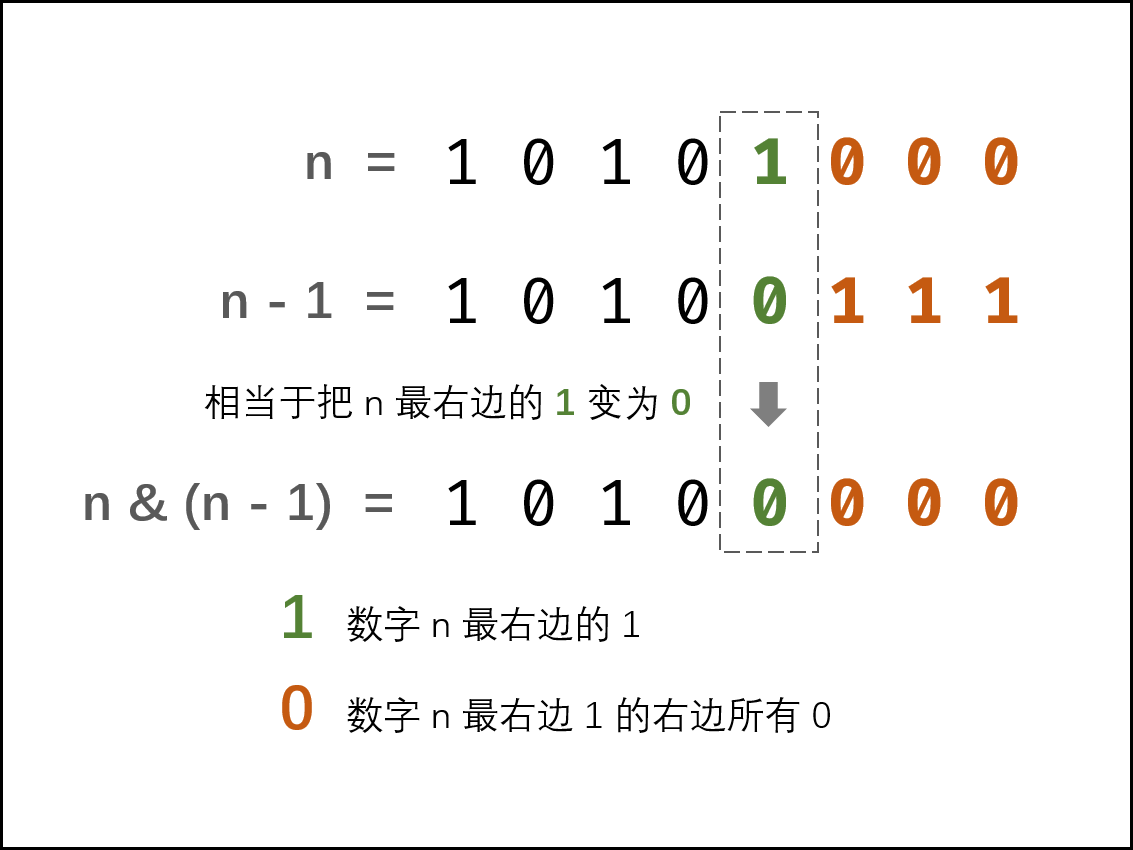
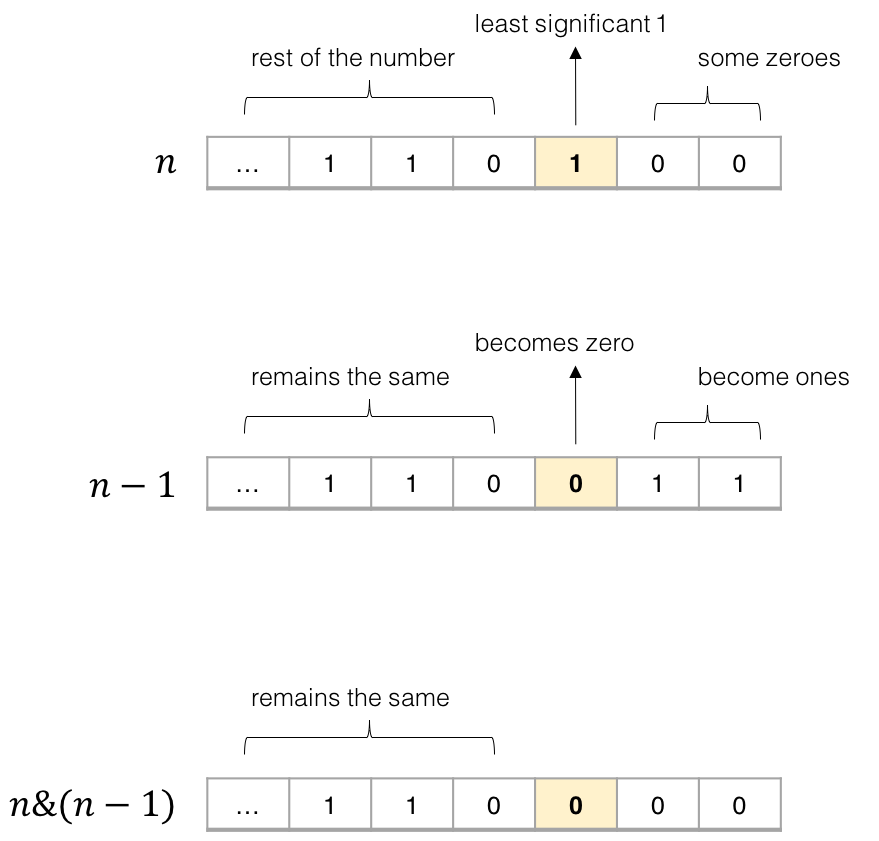
图片 1. 将 n 和 n-1 做与运算会将最低位的 1 变成 0

在二进制表示中，数字 n 中最低位的 1 总是对应 n - 1 中的 0 。因此，将 n 和 n - 1 与运算总是能把 n 中最低位的 1 变成 0 ，并保持其他位不变。

比如下面这两对数：

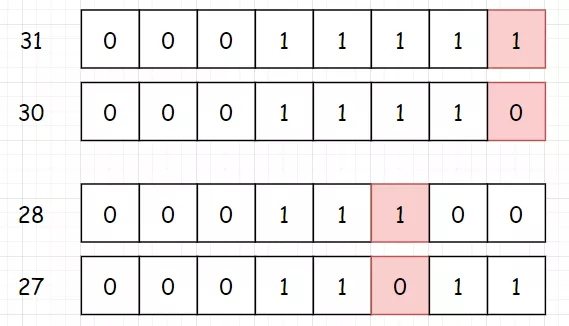
肯定有人又是看的一脸懵逼，我们拿 11 举个例子：（注意最后一位 1 变成 0 的过程）

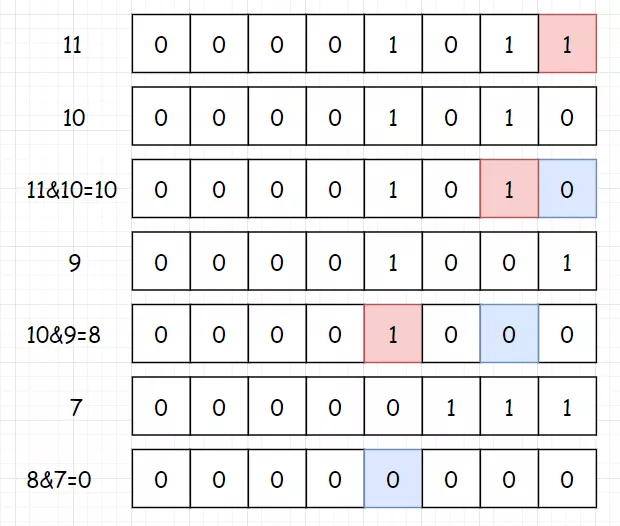
使用这个小技巧，代码变得非常简单。

Java

public int hammingWeight(int n) {

    int sum = 0;  // 用来存放 1 的个数

    while (n != 0) {
        sum++;
        n &= (n - 1);
    }
    return sum;
}

Java内置函数：1 的个数

public int hammingWeight(int n) {
    return Integer.bitCount(n);
}

异或相消（异或运算的特性）

我们先来看下异或的数学性质（数学里异或的符号是 \(\oplus\)）：

• 交换律：\(p \oplus q = q \oplus p\)
• 结合律：\(p \oplus (q \oplus r) = (p \oplus q) \oplus r\)
• 恒等率：\(p \oplus 0 = p\)
• 归零率：\(p \oplus p = 0\)

异或运算有以下三个性质。

1. 任何数和 0 做异或运算，结果仍然是原来的数，即 \(a \oplus 0=a\)。
2. 任何数和其自身做异或运算，结果是 0，即 \(a \oplus a=0\)。
3. 异或运算满足交换律和结合律，即 \(a \oplus b \oplus a=b \oplus a \oplus a=b \oplus (a \oplus a)=b \oplus0=b\)。

假设数组中有 2m+1 个数，其中有 m 个数各出现两次，一个数出现一次。令 \(a_{1}\)、\(a_{2}\)、\(\ldots\)…、\(a_{m}\) 为出现两次的 m 个数，\(a_{m+1}\) 为出现一次的数。根据性质 3，数组中的全部元素的异或运算结果总是可以写成如下形式：

\[(a_{1} \oplus a_{1}) \oplus (a_{2} \oplus a_{2}) \oplus \cdots \oplus (a_{m} \oplus a_{m}) \oplus a_{m+1}\]

根据性质 2 和性质 1，上式可化简和计算得到如下结果：

\[0 \oplus 0 \oplus \cdots \oplus 0 \oplus a_{m+1}=a_{m+1}\]

因此，数组中的全部元素的异或运算结果即为数组中只出现一次的数字。

下面我们来举个例子吧：
假如我们有 [21,21,26] 三个数，是下面这样：

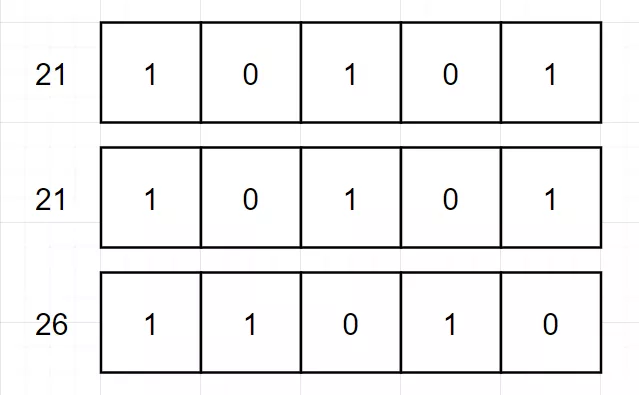
回想一下，之所以能用“异或”，其实我们是完成了一个 同一位上有 2 个 1 清零 的过程。上面的图看起来可能容易，如果是这样 (下图应为 26^21)：

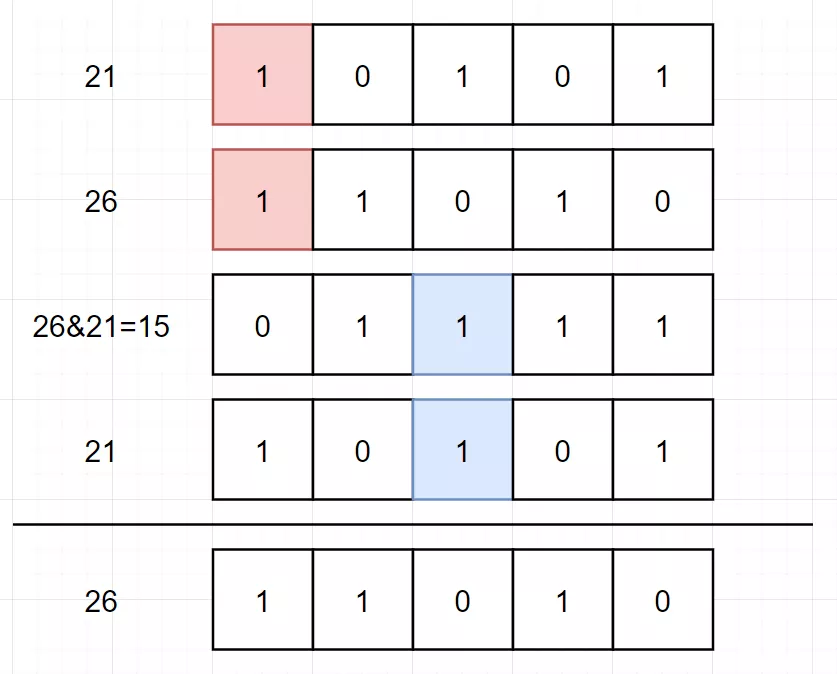
Java

class Solution {
    public int singleNumber(int[] nums) {
        int single = 0;
        for (int num : nums) {
            single ^= num;
        }
        return single;
    }
}

实例

位1的个数

编写一个函数，输入是一个无符号整数（以二进制串的形式），返回其二进制表达式中数字位数为 ‘1‘ 的个数（也被称为汉明重量）。

提示：

• 请注意，在某些语言（如 Java）中，没有无符号整数类型。在这种情况下，输入和输出都将被指定为有符号整数类型，并且不应影响您的实现，因为无论整数是有符号的还是无符号的，其内部的二进制表示形式都是相同的。
• 在 Java 中，编译器使用二进制补码记法来表示有符号整数。因此，在上面的 示例 3 中，输入表示有符号整数 -3。

进阶：

• 如果多次调用这个函数，你将如何优化你的算法？

示例 1：

输入：00000000000000000000000000001011
输出：3
解释：输入的二进制串 00000000000000000000000000001011 中，共有三位为 ‘1‘。

示例 2：

输入：00000000000000000000000010000000
输出：1
解释：输入的二进制串 00000000000000000000000010000000 中，共有一位为 ‘1‘。

示例 3：

输入：11111111111111111111111111111101
输出：31
解释：输入的二进制串 11111111111111111111111111111101 中，共有 31 位为 ‘1‘。

提示：
输入必须是长度为 32 的 二进制串。

答案

方法 1：循环和位移动

算法

这个方法比较直接。我们遍历数字的 32 位。如果某一位是 1 ，将计数器加一。

我们使用 位掩码 来检查数字的第 \(i^{th}\) 位。一开始，掩码 m=1 因为 1 的二进制表示是

\[0000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0001\]
0000 0000 0000 0000 0000 0000 0000 0001

显然，任何数字跟掩码 11 进行逻辑与运算，都可以让我们获得这个数字的最低位。检查下一位时，我们将掩码左移一位。

\[0000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0010\]
0000 0000 0000 0000 0000 0000 0000 0010

并重复此过程。

Java

public int hammingWeight(int n) {
    int bits = 0;
    int mask = 1;
    for (int i = 0; i < 32; i++) {
        if ((n & mask) != 0) {
            bits++;
        }
        mask <<= 1;
    }
    return bits;
}

复杂度分析

• 时间复杂度：\(O(1)\)。运行时间依赖于数字 n 的位数。由于这题中 n 是一个 32 位数，所以运行时间是 \(O(1)\) 的。

• 空间复杂度：\(O(1)\)。没有使用额外空间。

逐位判断
根据 与运算 定义，设二进制数字 n ，则有：

• 若 \(n \& 1 = 0\)，则 n 二进制 最右一位 为 00 ；
• 若 \(n \& 1 = 1\)，则 n 二进制 最右一位 为 11 。

根据以上特点，考虑以下 循环判断 ：

1. 判断 n 最右一位是否为 1 ，根据结果计数。
2. 将 n 右移一位（本题要求把数字 n 看作无符号数，因此使用 无符号右移 操作）。

算法流程：

1. 初始化数量统计变量 res = 0。
2. 循环逐位判断： 当 n = 0 时跳出。
3. res += n & 1 ： 若 \(n \& 1 = 1\) ，则统计数 res 加一。
4. n >>= 1 ： 将二进制数字 n 无符号右移一位（ Java 中无符号右移为 ">>>" ） 。
5. 返回统计数量 res。

public class Solution {
    public int hammingWeight(int n) {
        int res = 0;
        while(n != 0) {
            res += n & 1;  // 遍历
            n >>>= 1;  // 无符号右移
        }
        return res;
    }
}

方法 2：位操作的小技巧

算法

我们可以把前面的算法进行优化。我们不再检查数字的每一个位，而是不断把数字最后一个 1 反转，并把答案加一。当数字变成 0 的时候偶，我们就知道它没有 1 的位了，此时返回答案。

这里关键的想法是对于任意数字 n ，将 n 和 n - 1 做与运算，会把最后一个 1 的位变成 0 。为什么？考虑 n 和 n - 1 的二进制表示。

巧用 \(n \& (n - 1)\)
\((n - 1)\) 解析： 二进制数字 n 最右边的 1 变成 0 ，此 1 右边的 0 都变成 1 。
\(n \& (n - 1)\) 解析： 二进制数字 n 最右边的 1 变成 0 ，其余不变。

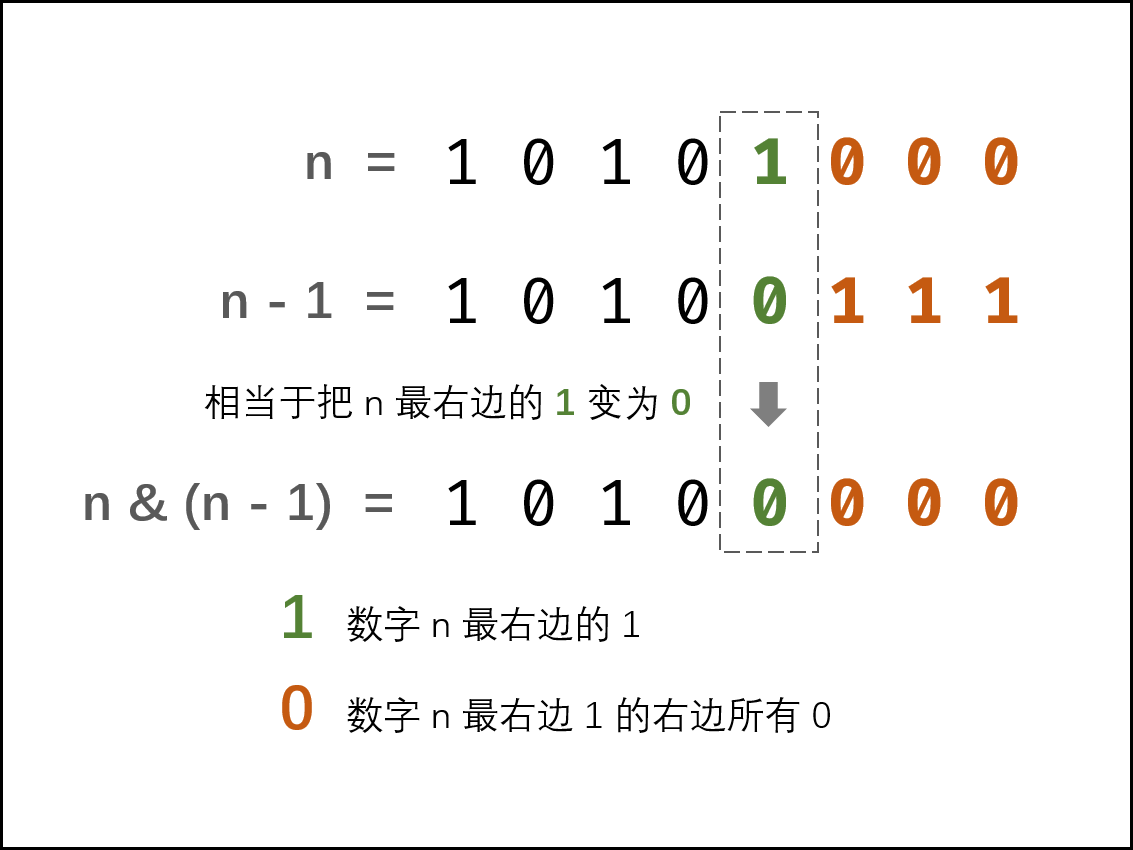
图片 1. 将 n 和 n-1 做与运算会将最低位的 1 变成 0

在二进制表示中，数字 n 中最低位的 1 总是对应 n - 1 中的 0 。因此，将 n 和 n - 1 与运算总是能把 n 中最低位的 1 变成 0 ，并保持其他位不变。

使用这个小技巧，代码变得非常简单。

Java

public int hammingWeight(int n) {
    int sum = 0;
    while (n != 0) {
        sum++;
        n &= (n - 1);
    }
    return sum;
}

复杂度分析

• 时间复杂度：\(O(1)\)。运行时间与 n 中位为 1 的有关。在最坏情况下，n 中所有位都是 1 。对于 32 位整数，运行时间是 \(O(1)\) 的。

• 空间复杂度：\(O(1)\)。没有使用额外空间。

只出现一次的数字

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

说明：

你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？

示例 1:

输入: [2,2,1]
输出: 1

示例 2:

输入: [4,1,2,1,2]
输出: 4

答案

方法一：位运算
如果不考虑时间复杂度和空间复杂度的限制，这道题有很多种解法，可能的解法有如下几种。

• 使用集合存储数字。遍历数组中的每个数字，如果集合中没有该数字，则将该数字加入集合，如果集合中已经有该数字，则将该数字从集合中删除，最后剩下的数字就是只出现一次的数字。

• 使用哈希表存储每个数字和该数字出现的次数。遍历数组即可得到每个数字出现的次数，并更新哈希表，最后遍历哈希表，得到只出现一次的数字。

• 使用集合存储数组中出现的所有数字，并计算数组中的元素之和。由于集合保证元素无重复，因此计算集合中的所有元素之和的两倍，即为每个元素出现两次的情况下的元素之和。由于数组中只有一个元素出现一次，其余元素都出现两次，因此用集合中的元素之和的两倍减去数组中的元素之和，剩下的数就是数组中只出现一次的数字。

上述三种解法都需要额外使用 \(O(n)\) 的空间，其中 n 是数组长度。

如何才能做到线性时间复杂度和常数空间复杂度呢？

答案是使用位运算。对于这道题，可使用异或运算 \(\oplus\)。异或运算有以下三个性质。

任何数和 0 做异或运算，结果仍然是原来的数，即 \(a \oplus 0=a\)。
任何数和其自身做异或运算，结果是 0，即 \(a \oplus a=0\)。
异或运算满足交换律和结合律，即 \(a \oplus b \oplus a=b \oplus a \oplus a=b \oplus (a \oplus a)=b \oplus0=b\)。

假设数组中有 2m+1 个数，其中有 m 个数各出现两次，一个数出现一次。令 \(a_{1}\)、\(a_{2}\)、\(\ldots\)…、\(a_{m}\) 为出现两次的 m 个数，\(a_{m+1}\) 为出现一次的数。根据性质 3，数组中的全部元素的异或运算结果总是可以写成如下形式：

\[(a_{1} \oplus a_{1}) \oplus (a_{2} \oplus a_{2}) \oplus \cdots \oplus (a_{m} \oplus a_{m}) \oplus a_{m+1}\]

根据性质 2 和性质 1，上式可化简和计算得到如下结果：

\[0 \oplus 0 \oplus \cdots \oplus 0 \oplus a_{m+1}=a_{m+1}\]

因此，数组中的全部元素的异或运算结果即为数组中只出现一次的数字。

Java

class Solution {
    public int singleNumber(int[] nums) {
        int single = 0;
        for (int num : nums) {
            single ^= num;
        }
        return single;
    }
}

复杂度分析

• 时间复杂度：\(O(n)\)，其中 n 是数组长度。只需要对数组遍历一次。

• 空间复杂度：\(O(1)\)。

剑指 Offer 56 - II. 数组中数字出现的次数 II

在一个数组 nums 中除一个数字只出现一次之外，其他数字都出现了三次。请找出那个只出现一次的数字。

示例 1：

输入：nums = [3,4,3,3]
输出：4

示例 2：

输入：nums = [9,1,7,9,7,9,7]
输出：1

位运算答案

// 虽然位运算很麻烦，但是我也得试试啊
class Solution {
    public int singleNumber(int[] nums) {

        // 位运算有点麻烦

        // 把所有数的二进制位相加，对每一位取余3，那么剩下来的就是我们需要找的数字了
        int[] counts = new int[32]; // 用来存储答案数字的32位二进制
        
        // 遍历数组中的所有数，将他们的二进制位相加，存起来
        for(int num : nums) {
            // 从0到31，从低位到高位
            for(int j = 0; j < 32; j++) {
                counts[j] += num & 1;
                num >>>= 1;
            }
        }

        // 从高位开始，把每一位二进制 % 3
        int res = 0;    // 结果答案
        for(int i = 31; i >= 0; i--) {
            // 先移位再加个位，就如 sum += sum * 10 + 个位
            res <<= 1;
            res |= counts[i] % 3;
        }
        return res;

    }
}

哈希表答案

class Solution {
    public int singleNumber(int[] nums) {

        // 位运算有点麻烦

        // 哈希表
        Map<Integer, Integer> map = new HashMap<>();

        for (int i = 0; i < nums.length; i++) {
            
            int count = map.getOrDefault(nums[i], 0) + 1;

            map.put(nums[i], count);
        }

        for (int i = 0; i < nums.length; i++) {
            
            int count = map.getOrDefault(nums[i], 0);
            if (count == 1) {
                return nums[i];
            }
        }

        return 0;
    }
}

两数之和

第268题：不使用运算符 + 和 - ，计算两整数 a 、b 之和。

答案

位运算的题，大部分都有一些特别的技巧，只要能掌握这些技巧，对其拼装组合，就可以破解一道道的题目。很多人说那些技巧想不到，我觉得是因为没有认真的去学习和记忆。你要相信，基本上所有人最开始都是不会的，只是后来他们通过努力学会了记住了，而你因为没努力一直停留在不会而已。不要觉得那些一眼看到题就能想到解法的人有多么了不起。“无他，唯手熟尔！”

下面这两个技巧大家需要记住，这也是讲解本题的目的：

• “异或”是一个无进位加法，说白了就是把进位砍掉。比如01^01=00。

• “与”可以用来获取进位，比如01&01=01，然后再把结果左移一位，就可以获取进位结果。

根据上面两个技巧，假设有 12+7：

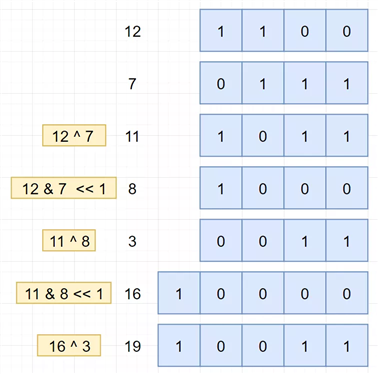
根据分析，完成题解：

//JAVA
class Solution {
    public int getSum(int a, int b){
        while(b != 0){
            int temp = a ^ b;
            b = (a & b) << 1;
            a = temp;
        }
        return a;
    }
}

剑指 Offer 65. 不用加减乘除做加法

写一个函数，求两个整数之和，要求在函数体内不得使用 “+”、“-”、“*”、“/” 四则运算符号。

示例:

输入: a = 1, b = 1
输出: 2

答案

//JAVA
class Solution {
    public int add(int a, int b) {
        // 该位都为1，&，则进位
        // 异或运算，^，非进位加

        // 我们使用temp来记录进位的位数二进制
        // 每次我们都将 非进位和 与 进位二进制 做非进位加法运算，直到没有进位为止（进位为0）
        while(b != 0) { // 当进位为 0 时跳出
            int temp = (a & b) << 1;  // temp = 进位
            a ^= b; // a = 非进位和
            b = temp; // b = 进位
        }
        return a;
    }
}

【算法】位运算技巧

原文：https://www.cnblogs.com/blknemo/p/14470610.html