TL；DR
WN(Weight Normalization):
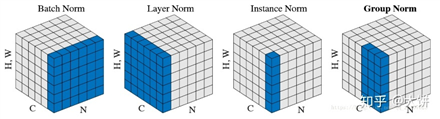
BN(Batch Normalization)：批样本单通道，对象为NHW
LN(Layer Normalization)：单样本全通道，对象为CHW
IN(Instance Normalization)：单样本单通道，对象为HW
GN(Group Normalization)：单样本批通道，对象为GH*W

权重归一化 WN（Weight Normalization）

权重归一化的重要目的是，避免模型过拟合。

• L1 正则的规范化目标是造成参数的稀疏化，就是争取达到让大量参数值取得 0 值的效果
• L2 正则的规范化目标是有效减小原始参数值的大小。
  有了这些规范目标，通过具体的规范化手段来改变参数值，以达到避免模型过拟合的目的。

批量归一化 BN（Batch Normalization）

Why does Batch Normalization work?

在深层网络训练的过程中，由于网络中参数变化而引起内部结点数据分布发生变化的这一过程，被称作内部协变量转移Internal Covariate Shift（ICF）。
假如我们要训练一个神经网络分类器，我们从训练数据中拿到两个明显分布不同的两个batch。当我们用这两个batch分别去训练神经网络的时候，就会由于训练batch分布的剧烈波动导致收敛速度慢，甚至是神经网络性能的下降。这就是在输入数据上的Covariate shift。
通常我们可以通过增大batch的大小，并充分对数据进行shuffle来保证每个batch的分布尽量接近原始数据的分布，从而减少Covariate shift带来的负面影响。

同样的对于神经网络的每一层的输入数据同样存在类似的问题，这就是Internal Covariate Shift。但是在训练过程中，神经网络的参数会不断地更新，会导致神经网络内部的输入输出分布的剧烈波动，我们并不能像处理输入数据那样去处理神经网络内部每一层的输入输出。
BN的提出就是为了解决这个问题的。将每一层的输入分布都归一化到均值为0，方差为1上，减少了所谓的 Internal Covariate Shift，从而稳定乃至加速了训练。

但是我们仔细思考，均值和方差相同，数据分布就一定相同或者相近吗，显然是不是的。不管哪一层的输入都不可能严格满足正态分布，从而单纯地将均值方差标准化无法实现标准分布 N(0, 1) ；其次，就算能做到 N(0, 1) ，这种诠释也无法进一步解释其他归一化手段（如 Instance Normalization、Layer Normalization）起作用的原因。

个人感觉。BN 的作用更像是多种因素的复合结果，比如对于我们主流的激活函数来说， [?1,1] 基本上都是非线性较强的区间，所以将输入弄成均值为 0、方差为 1，也能更充分地发挥激活函数的非线性能力，不至于过于浪费神经网络的拟合能力。

再比如我们对神经网络的训练数据，特别是图像数据进行预处理的时候都要进行所谓的“白化”操作，最常见的白化操作便采用PCA对数据进行白化操作，最后达到的效果如图所示：

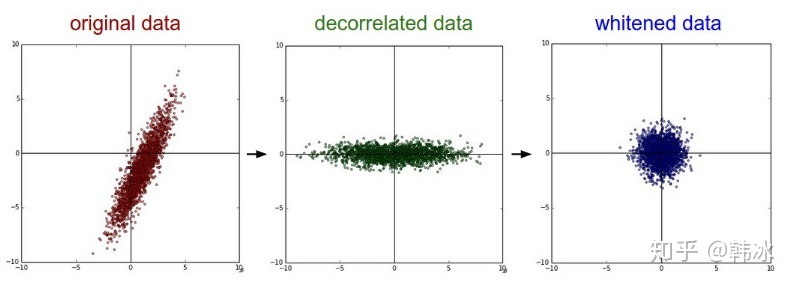
但是对于神经网络内部来说，做这样的白化操作代价过大，而且PCA操作也不是一个可微分的操作。所以我们用正则化操作来替代白化操作，也可以达到类似的效果，如图所示：

How does batch normalization work?

训练阶段

feature map： 包含 N 个样本，每个样本通道数为C，高为H，宽为W。对其求均值和方差时，将在 N、H、W 上操作，而保留通道C的维度。
具体来说，就是把第 1 个样本的第 1 个通道，加上第 2 个样本第 1 个通道 ...... 加上第 N 个样本第 1 个通道，求平均，得到通道 1 的均值。对所有通道都施加一遍这个操作，就得到了所有通道的均值和方差。

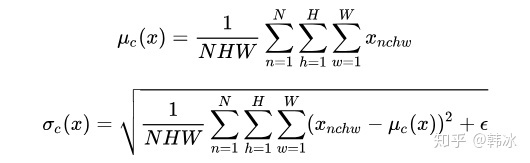
?最后我们将每个 pixel 对应的值减去均值，除以方差，就得到了规范化的结果。在此基础上，BN 还增加了两个可训练的参数 γ，β。所以最终的表达式为:

测试阶段

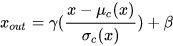
我们知道BN在每一层计算的均值与方差都是基于当前batch中的训练数据，但是这就带来了一个问题：我们在预测阶段，有可能只需要预测一个样本或很少的样本，没有像训练样本中那么多的数据，
此时均值与方差的计算一定是有偏估计，这个时候我们该如何进行计算呢？
利用BN训练好模型后，我们保留了每组mini-batch训练数据在网络中每一层的均值与方差。此时我们使用整个样本的统计量来对Test数据进行归一化，具体来说使用均值与方差的无偏估计：

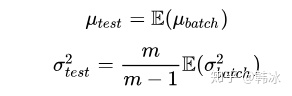
得到每个特征的均值与方差的无偏估计后，我们对test数据采用同样的normalization方法：

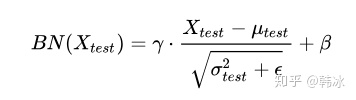
作用：

• BN对各种极端的超参数都有很强的适应能力。在训练的过程中使用BN我们完全可以使用较大的学习率加快收敛速度，而且不会影响模型最终的效果。BN会使得每层的数据的均值和方差控制在一定的范围内，上层网络不必不断去适应底层网络中的输入的变化，实现了层与层之间的解耦，允许每一层进行独立学习，会提高神经网络的学习速度。
• BN通过将每一层网络的输入进行normalization，保证输入分布的均值与方差固定在一定范围内，并在一定程度上缓解了梯度消失，加速了模型收敛；
• 并且BN使得网络对参数、激活函数更加具有鲁棒性，降低了神经网络模型训练和调参的复杂度；
• 最后BN训练过程中由于使用mini-batch的mean/variance作为总体样本统计量估计，引入了随机噪声，在一定程度上对模型起到了正则化的效果。

BN的思考

• BN以每个MiniBatch对每个特征进行规范化处理，这要求每个MiniBatch的统计量是整体统计量的近似估计，这就意味着每个MiniBatch和整体数据应该是近似同分布的，如此，如果Minibatch比较小的话，那么不同Batch之间的数据分布差异性会更大；
• 分布差距较小的MiniBatch的数据可以认为规范化处理给模型带来了噪声，可以增加模型的泛化能力；如果每个MiniBatch的数据分布差距较大，那么不同的MiniBatch的数据将会进行不同的数据变换，着会增加模型的训练难度；
• BN适用于每个MiniBatch的数据分布差距不大的情况，并且训练数据要进行充分的shuffle，不然效果反而变差，增大训练难度；
• BN不适用于动态的网络结构和RNN网络。
• BN由于基于MiniBatch的归一化统计量来代替全局统计量，相当于在梯度计算中引入了噪声，因此一般不适用与生成模型，强化学习等对噪声敏感的网络中。

import torch

class BatchNorm2d(torch.nn.Module):
    def __init__(self, channel, eps=1e-5, affine=True, momentum=0.9):
        super().__init__()

        # 初始化训练参数
        self.gamma = torch.nn.Parameter(torch.ones(1, channel, 1, 1))
        self.beta = torch.nn.Parameter(torch.zeros(1, channel, 1, 1))
        self.eps = eps
        self.affine = affine
        self.momentum = momentum

        self.register_buffer(‘running_mean‘, torch.zeros(channel))
        self.register_buffer(‘running_var‘, torch.ones(channel))

    def forward(self, input):
        # input shape must be (N, C, H, W)
        if self.training:
            means = input.mean((0, 2, 3), keepdim=True)
            vars = ((input-means)**2).sum((0, 2, 3), keepdim=True)
            self.running_mean = self.momentum * self.running_mean + (1-self.momentum) * means
            self.running_var = self.momentum * self.running_var + (1-self.momentum) * vars
        else:
            means = self.running_mean
            vars = self.running_var

        output = (input - means) / torch.sqrt(vars + self.eps)
        if self.affine:
            output =  output* self.gamma + self.beta
        return output

层归一化 LN（Layer Normalization）

LN一般只用于RNN的场景下，在CNN中LN规范化效果不如BN,WN,GN,IN的
LN与BN的区别

• LN针对当个训练样本进行规范化，不像BN那样依赖于一个MiniBatch的数据，因此避免了不同样本之间的相互影响，可以适用于动态网络场景，RNN和自然语言处理领域
• LN不需要保存MiniBatch的均值和方差，相比BN计算量更小
• BN针对单个神经元进行规范化，不同神经元的输入经过平移和缩放使不同神经元的分布在不同的区间中，LN对于整个一层的神经元进行转换，所有的输入全部控制在同一个区间范围内。在CNN中，假设输入的是一张图片，同一层的输入特征表征着不同的特征，例如有的位置神经元表征的是颜色信息，有的位置神经元表征的是形状信息，那么这个时候BN是更合适的，使不同的特征信息进行分别处理，但是如果这种输入使用LN处理，将一个样本的所有特征的分布全部标准化到一个统一的区间，显然会降低模型的表达能力。

样本归一化 IN（Instance Normalization）

InstanceNormalization主要是针对CNN设计，并且是为了弥补BN的对batch的依赖。
InstanceNormalization对于图像生成任务效果明显优于BN，在图像分类上不如BN。

分组归一化 GN（Group Normalization）

GN在要求batch比较小的场景下或者目标检测，视频分类等任务由于BN

参考博客：
深入理解Batch Normalization
深度学习-Normalization

Normalization总结（BN-LN-IN-GN）

原文：https://www.cnblogs.com/Tsingwaa/p/14586091.html