作者:elfin 资料来源:官网pytorch1.6.0
各种学习率曲线可视化参考:python黑洞网
torch.optim.lr_scheduler.LambdaLR
参数:
案例:
>>> # Assuming optimizer has two groups.
>>> lambda1 = lambda epoch: epoch // 30
>>> lambda2 = lambda epoch: 0.95 ** epoch
>>> scheduler = LambdaLR(optimizer, lr_lambda=[lambda1, lambda2])
>>> for epoch in range(100):
>>> train(...)
>>> validate(...)
>>> scheduler.step()
torch.optim.lr_scheduler.MultiplicativeLR
参数:
optimizer(Optimizer): 优化器;
lr_lambda(function or list):传递给优化器每个分组(optimizer.param_groups)的自定义函数或函数列表.
last_epoch(int):最后一个epoch的索引,默认为-1.
verbose(bool):默认为False;如果为True,每次更新打印一条标准输出信息.
案例:
>>> lmbda = lambda epoch: 0.95
>>> scheduler = MultiplicativeLR(optimizer, lr_lambda=lmbda)
>>> for epoch in range(100):
>>> train(...)
>>> validate(...)
>>> scheduler.step()
每个参数组的学习速率都会被gamma逐级递减。注意,这种衰减可能与此调度程序外部的学习速率的其他更改同时发生。当last_epoch=-1时,将初始lr设置为lr。
torch.optim.lr_scheduler.StepLR
参数:
更新公式:
torch.optim.lr_scheduler.MultiStepLR
? 当epoch数达到某个里程碑时,用gamma衰减每个参数组的学习率。请注意,这样的衰减可以与来自此调度器外部的学习速率的其他更改同时发生。当last_epoch=-1时,将初始lr设置为lr。
参数:
调整策略:
self.lr * self.gamma ** bisect_right(self.milestones, epoch)
案例:
>>> # Assuming optimizer uses lr = 0.05 for all groups
>>> # lr = 0.05 if epoch < 30
>>> # lr = 0.005 if 30 <= epoch < 80
>>> # lr = 0.0005 if epoch >= 80
>>> scheduler = MultiStepLR(optimizer, milestones=[30,80], gamma=0.1)
>>> for epoch in range(100):
>>> train(...)
>>> validate(...)
>>> scheduler.step()
注:bisect_right测试
>>> from bisect import bisect_right
>>> milestones = [30, 80]
>>> print(bisect_right(milestones, 10))
Out[0] 0
>>> print(bisect_right(milestones, 50))
Out[0] 1
>>> print(bisect_right(milestones, 200))
Out[0] 2
注意这里实际上是分了几段在控制gamma因子的指数,里程牌参数记录的是分段的节点。
torch.optim.lr_scheduler.ExponentialLR
将每个参数组的学习率按gamma每个epoch衰减一次。当last_epoch=-1时,将初始lr设置为lr。
参数:
torch.optim.lr_scheduler.CosineAnnealingLR
SGDR:带有热重启的随机梯度下降
CLR:周期性学习率
SGDR与CLR比较类似。
参考资料:https://www.jianshu.com/p/40adad7cb50d
? https://blog.csdn.net/qq_38410428/article/details/88061738
? 使用余弦退火计划设置每个参数组的学习速率,其中\(\eta_{max}\)是初始化的学习率,\(T_{cur}\)是自上次重新启动以来的epoch数:
当 last_epoch=-1时,则初始化学习率\(lr\)。注意,由于调度是递归定义的,因此其他操作符可以在此调度程序之外同时修改学习速率。如果学习率仅由该调度器设置,则每个步骤的学习率将变为:
在SGDR中提出了一种新的方法:带Warm Restarts重启的随机梯度下降。注意,这只实现了SGDR的余弦退火部分,而不是重新启动(没有周期性的热重启初始化学习率)。
参数:
torch.optim.lr_scheduler.ReduceLROnPlateau
? 当指标停止改善时,降低学习率。一旦学习停滞,模型通常受益于将学习率降低2-10倍。这个调度器读取一个度量量,如果在“耐心”的时间段上看不到改进,那么学习率就会降低。
参数:
optimizer(Optimizer): 优化器;
mode(str):\(min、max\)中的一个,默认为\(min\)。在最小模式下,当监控量停止减少时,lr将减小;在最大模式下,当监控量停止增加时,lr将减小.
factor(float):默认0.1,\(new\_lr=lr \times factor\).
patience(int):学习率降低后没有改善的epoch数。例如,如果patience=2,那么我们将忽略前两个没有改善的epoch,并且如果损失仍然没有改善,那么只会在第三个epoch之后降低LR。默认值:10.
threshold(float):衡量最佳的阈值,要只关注显著的变化.
threshold_mode(str):["rel", "abs"]其中之一,分别为相对模式、绝对模式。"rel"模式下,如果在"max" mode下有:\(dynamic\_threshold = best \times ( 1 + threshold)\). 在"min" mode下有:\(dynamic\_threshold = best \times ( 1 -threshold)\).
在"abs"模式下,如果在"max" mode下有:\(dynamic\_threshold = best + threshold\);
如果在"min" mode下有:\(dynamic\_threshold = best - threshold\);
cooldown(int):学习率降低后恢复正常操作前要等待的epoch数,默认为0.
min_lr(float or list):标量标量或标量列表。所有参数组或每组学习率的下限.
eps(float):最小衰减应用于lr。如果新旧lr之间的差异小于eps,则忽略更新。默认为\(10^{-8}\).
verbose(bool):默认为False;如果为True,每次更新打印一条标准输出信息.
torch.optim.lr_scheduler.CyclicLR
? 根据周期性学习率策略(CLR)设置每个参数组的学习率。该策略以恒定的频率在两个边界之间循环学习速率。参考文献: Cyclical Learning Rates for Training Neural Networks. 两个边界之间的距离可以在每次迭代或每次循环的基础上进行缩放。
? 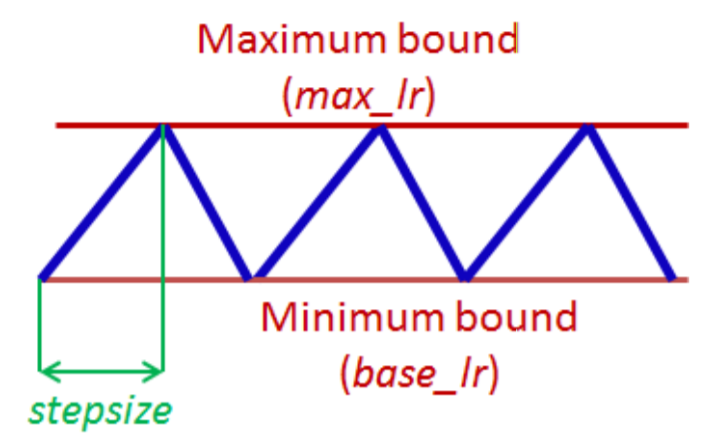
? 循环学习率策略改变每批的学习率后。在一个batch被用于train之前,应该先调用\(step\)方法。
此类内置了三种策略,正如论文中提出的那样:
参数:
optimizer(Optimizer): 优化器;
base_lr(float or list):初始学习率,即每个参数组在循环中的下界。
max_lr(float or list):每个参数组在循环中的学习速率上限。在功能上,它定义了周期振幅(max_lr-base_lr)。任何周期的lr都是base_lr和缩放振幅的总和;因此,根据缩放函数scaling,实际上可能无法达到max_lr。
step_size_up (int):在学习率增加的半个周期中的训练迭代次数。默认值:2000.
step_size_down (int):在学习率增加的半个周期中的训练迭代次数。默认值:None,为None时默认与step_size_up一致.
mode(str): {triangular, triangular2, exp_range} 可选,默认triangular。值与上面详述的策略相对应。如果scale_fn不是None,则忽略此参数.
gamma (float):默认1.0。“exp_range”缩放函数中的常量:\(gamma^{cycle\ iterations}\).
scale_fn:缩放函数。
scale_mode(str):{‘cycle’, ‘iterations’}可选。定义是根据循环数还是循环迭代来计算scale_fn。默认‘cycle’.
cycle_momentum (bool):如果为真,则动量循环在“基本动量”和“最大动量”倒数之间。默认值:True.
base_momentum(float or list):基本动量.
max_momentum(float or list):最大动量.
last_epoch(int):最后一个epoch的索引,默认为-1.
verbose(bool):默认为False;如果为True,每次更新打印一条标准输出信息.
案例:
>>> optimizer = torch.optim.SGD(model.parameters(), lr=0.1, momentum=0.9)
>>> scheduler = torch.optim.lr_scheduler.CyclicLR(optimizer, base_lr=0.01, max_lr=0.1)
>>> data_loader = torch.utils.data.DataLoader(...)
>>> for epoch in range(10):
>>> for batch in data_loader:
>>> train_batch(...)
>>> scheduler.step()
? 根据 1cycle 学习率策略设置每个参数组的学习率。 1cycle 策略将学习速率从初始学习速率退火到某个最大学习速率,然后从该最大学习速率退火到远低于初始学习速率的某个最小学习速率。
参考文献: Super-Convergence: Very Fast Training of Neural Networks Using Large Learning Rates.
? 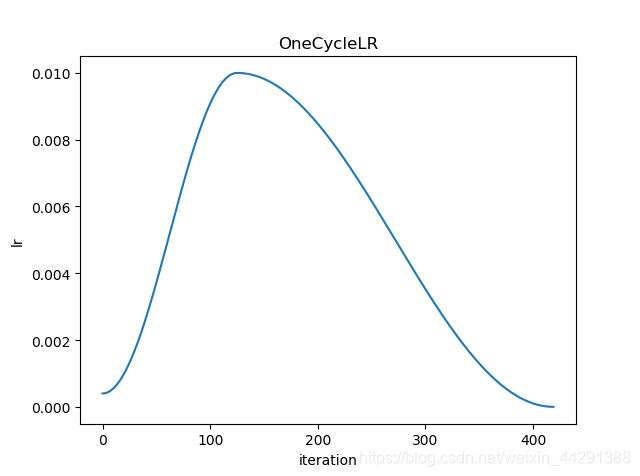
图片来源于:python黑洞网
? 1cycle 学习率策略会在每个batch之后更改学习率。每个batch数据在训练之前都要先调用\(step\)方法。
还要注意,循环中的总步数可以通过以下两种方式之一确定(按优先顺序列出):
参数:
案例:
>>> data_loader = torch.utils.data.DataLoader(...)
>>> optimizer = torch.optim.SGD(model.parameters(), lr=0.1, momentum=0.9)
>>> scheduler = torch.optim.lr_scheduler.OneCycleLR(optimizer, max_lr=0.01, steps_per_epoch=len(data_loader), epochs=10)
>>> for epoch in range(10):
>>> for batch in data_loader:
>>> train_batch(...)
>>> scheduler.step()
torch.optim.lr_scheduler.CosineAnnealingWarmRestarts
当\(T_{cur}=T_{i}\), 令 \(\eta_t = \eta_{min}\). 当\(T_{cur}=0\),重启学习率,令:\(\eta_t=\eta_{max}\).
参考文献: SGDR: Stochastic Gradient Descent with Warm Restarts.
参数:
案例:
>>> scheduler = CosineAnnealingWarmRestarts(optimizer, T_0, T_mult)
>>> iters = len(dataloader)
>>> for epoch in range(20):
>>> for i, sample in enumerate(dataloader):
>>> inputs, labels = sample[‘inputs‘], sample[‘labels‘]
>>> optimizer.zero_grad()
>>> outputs = net(inputs)
>>> loss = criterion(outputs, labels)
>>> loss.backward()
>>> optimizer.step()
>>> scheduler.step(epoch + i / iters)
这个函数可以交叉调用。
>>> scheduler = CosineAnnealingWarmRestarts(optimizer, T_0, T_mult)
>>> for epoch in range(20):
>>> scheduler.step()
>>> scheduler.step(26)
>>> scheduler.step() # scheduler.step(27), instead of scheduler(20)
完! pytorch-1.6.0
原文:https://www.cnblogs.com/dan-baishucaizi/p/14586449.html