LeetCode（#48）：旋转数组

一、前言

本题为LeetCode第48题，是一道 数组 相关的算法题，难度中等。

本题链接：#48. 旋转数组

二、题目

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。

示例1：

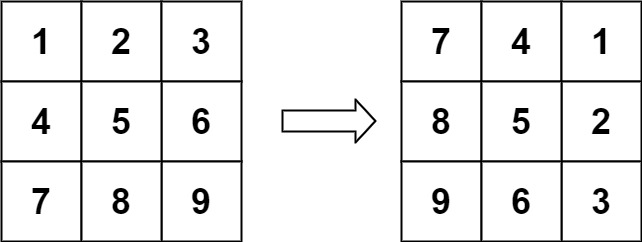
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例二：

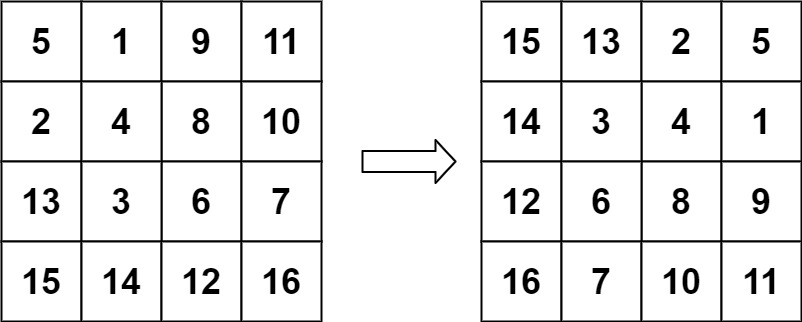
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

三、思路

首先分析题目要求，必须原地旋转图像，表示不能创建一个新矩阵作为旋转后的矩阵，要直接修改原矩阵。本文的解题思路有两种。

• 解题思路一：先将矩阵进行转置操作，再进行左右镜像操作，即可将矩阵旋转90°。

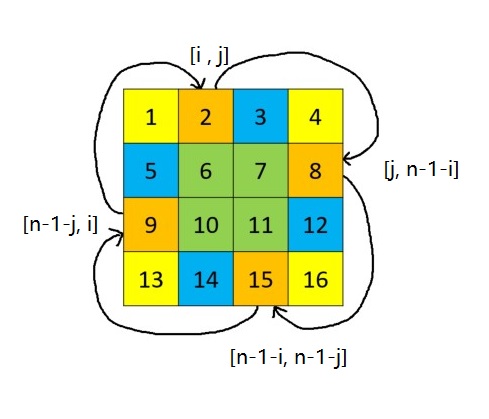
• 解题思路二：将矩阵外圈四个边上的对应元素进行90°的旋转操作，如下图所示，相同颜色代表相互交换的四个位置；外圈交换完位置后，对内圈的矩阵进行相同操作。

四、Java代码

• 思路一代码实现

public class solution {
    public void rotate(int[][] matrix) {
        
        int n = matrix.length;
        int tmp = 0;
        
        // 1.转置（这是矩阵转置的Java代码，基本矩阵操作，可以记忆一下）
        for(int i = 0; i < n; i++) {
            for(int j = 0; j < i; j++) {
                tmp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = tmp;
            }
        }
        
        // 2.镜像（同上）
        for(int i = 0; i < n; i++) {
            for(int j = 0; j < n/2; j++) {
                tmp = matrix[i][j];
                matrix[i][j] = matrix[i][n-1-j];
                matrix[i][n-1-j] = tmp;
            }
        }
        
    }
}

• 思路二代码实现

   public class solution {
       public void rotate(int[][] matrix) {
           
           int n = matrix.length;
           int tmp = 0;
           
           // 每一圈的上面那行元素先用tmp存储起来，之后进行顺序赋值
           // 仔细观察可以发现，任意元素进行90°旋转后，其纵坐标变成横坐标，n-1-横坐标变成转换后的纵坐标。即转换前坐标[i,j]，转换后为[j,n-1-i]
           // 该规律的图解在上图。个人认为该规律的原因，可以用对应元素与矩阵的四个角上的元素的相对位置进行分析
           for(int i = 0; i < n/2; i++) {
               for(int j = i; j < n-1-i; j++) {
                   tmp = matrix[i][j];
                   matrix[i][j] = matrix[n-1-j][i];
                   matrix[n-1-j][i] = matrix[n-1-i][n-1-j];
                   matrix[n-1-i][n-1-j] = matrix[j][n-1-i];
                   matrix[j][n-1-i] = tmp;
               }
           }
       }
   }

?

LeetCode（#48）：旋转数组

原文：https://www.cnblogs.com/ziqin/p/14587109.html