线性方程组 Ax =b 除了高斯消元法以外,还有其它的迭代解法,这里我们说的是共轭梯度法。
这里只针对 A 满足 对称 ( ), 正定(即
),并且是实系数的,那么我们可以用 梯度下降 和 共轭梯度 来解线性方程组 :
向量 和
是共轭的 (相对于A )如果满足:
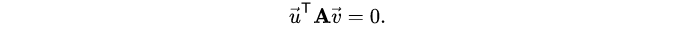
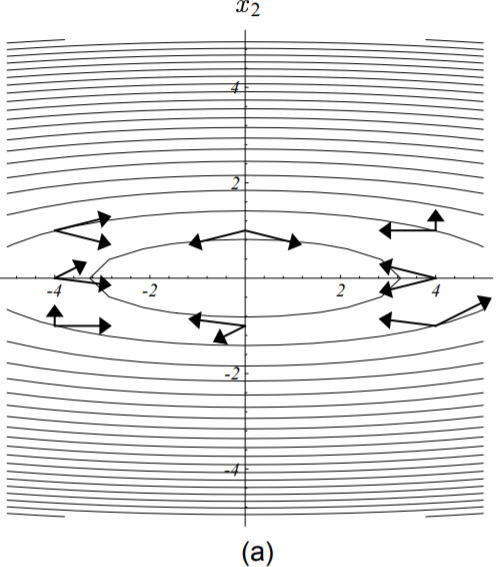
下图两两向量都是针对所在梯度处的矩阵‘共轭’的:
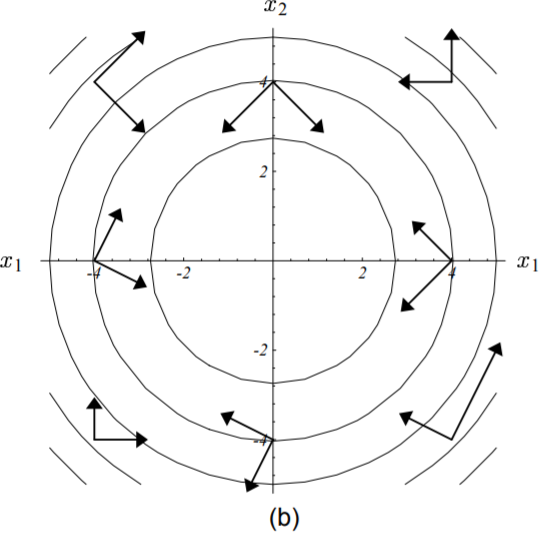
把梯度变换一下,就可以看出‘共轭’其实也就是某种正交:
=============================================
共轭梯度法解:
算法步骤:(from wiki)

---------------------------------------------
python代码:(源于:Baselines:https://github.com/openai/baselines(强化学习算法))
import numpy as np """共轭梯度下降""" def cg(f_Ax, b, cg_iters=10, callback=None, verbose=False, residual_tol=1e-10): """ Demmel p 312 """ p = b.copy() r = b.copy() x = np.zeros_like(b) rdotr = r.dot(r) fmtstr = "%10i %10.3g %10.3g" titlestr = "%10s %10s %10s" if verbose: print(titlestr % ("iter", "residual norm", "soln norm")) for i in range(cg_iters): if callback is not None: callback(x) if verbose: print(fmtstr % (i, rdotr, np.linalg.norm(x))) z = f_Ax(p) v = rdotr / p.dot(z) x += v*p r -= v*z newrdotr = r.dot(r) mu = newrdotr/rdotr p = r + mu*p rdotr = newrdotr if rdotr < residual_tol: break if callback is not None: callback(x) if verbose: print(fmtstr % (i+1, rdotr, np.linalg.norm(x))) # pylint: disable=W0631 return x
=============================================
参考:
图来源:
------------------------------------------------------------------------------
原文:https://www.cnblogs.com/devilmaycry812839668/p/14587729.html