P3382 【模板】三分法

时间限制 1.00s
内存限制 128.00MB

题目描述

如题，给出一个\(N\)次函数，保证在范围\([l, r]\)内存在一点\(x\)，使得\([l, x]\)上单调增，\([x, r]\)上单调减。试求出\(x\)的值。

输入格式

第一行一次包含一个正整数\(N\)和两个实数\(l,r\)，含义如题目描述所示。

第二行包含\(N+1\)个实数，从高到低依次表示该\(N\)次函数各项的系数。

输出格式

输出为一行，包含一个实数，即为\(x\)的值。若你的答案与标准答案的相对或绝对误差不超过\(10^{-5}\)则算正确。

输入输出样例

输入 #1

3 -0.9981 0.5
1 -3 -3 1

输出 #1

-0.41421

说明/提示

对于\(100\%\)的数据，\(6 \le N \le 13\)，函数系数均在\([?100,100]\)内且至多\(15\)位小数，\(|l|,|r|\leq 10\)且至多\(15\)位小数。\(l\leq r\)。

【样例解释】

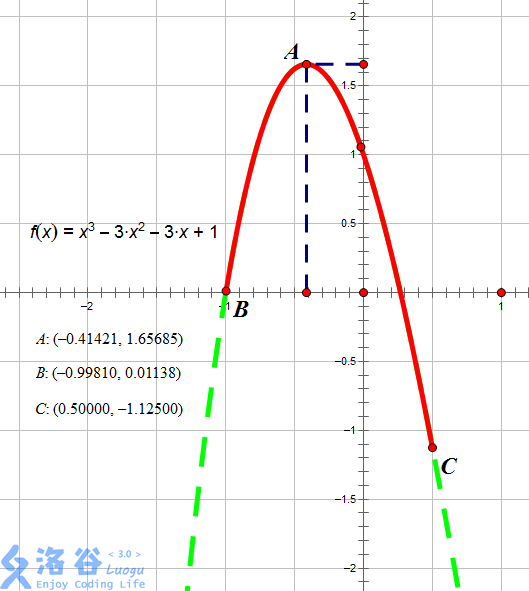
如图所示，红色段即为该函数\(f(x) = x^3 - 3 x^2 - 3x + 1\)在区间\([?0.9981,0.5]\)上的图像。

当\(x=?0.41421\)时图像位于最高点，故此时函数在\([l,x]\)上单调增，\([x,r]\)上单调减，故\(x=?0.41421\)，输出\(?0.41421\)。

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
double n,l,r,L,R,a[20];
double f(double x){
	double res=0;
	for(int i=n;i>=0;--i) res+=a[i]*pow(x,i);
	return res;
}
int main(){
	scanf("%lf %lf %lf",&n,&l,&r);
	for(int i=n;i>=0;--i) scanf("%lf",&a[i]);
	while(r-l>1e-6){
		L=l+(r-l)/3;
		R=r-(r-l)/3;
		if(f(L)<=f(R)) l=L;
		else r=R;
	}
	printf("%.5lf",l);
	return 0;
}

P3382 【模板】三分法

原文：https://www.cnblogs.com/Potrem/p/Luogu_P3382.html