Polynomial、项Term、因子Unit本人采用递归下降的思路,下面简述递归下降算法:
假设一个类A的字符串形式是"BCD"(拼接),B的形式是"x*E",c是sin(x),D是(A),E是+,那么我们要分析字符串A,就可以这样写
public A getA(){
A ans = new A();
B newB = getB();
C newC = getC();
D newD = getD();
ans.addB(newB); ans.addC(newC); ans.addD(newD);
return ans;
}
public B getB(){
B ans = new B();
if(接下来是"x*"){
走2步;
} else {
throw 格式错误异常;
}
E newE = getE();
ans.addE(newE);
return ans;
}
public C getC(){
C ans = null;
if(接下来是"sin(x)"){
ans = new C();
走6步;
} else {
throw 格式错误异常;
}
}
public D getD(){
D ans = null;
if(接下来是"("){
走1步;
} else {
throw 格式错误异常;
}
A newA = getA();
ans.addA(newA);
if(接下来是")"){
走1步
} else {
throw 格式错误异常;
}
return ans;
}
...//剩下的就不写了,主要思路已经阐释清楚
这样,从最大的一级,逐级递归的找更小的构成单元,直到找到以字符为匹配单元的最小单元,由此可以对符合一定语法的字符串进行全面分析
现在再看,我设计的递归下降其实糅合了递归下降和类的生成,这就使得耦合度过高,较为高明的办法应该是使用工厂模式,建立一个MFactory类,在递归下降中,将匹配到的字符串交由工厂生成一个相应的对象,而不是自己new一个出来
ExpressionString由于在递归下降的过程中,经常需要移动指针、判断字符,因此将这部分功能抽取出来作为一个新的工具类,减小递归下降类的复杂度
成员由一个String存放表达式,一个Integer存放当前位置
ExpressionString实现的方法主要是
public void moveSpace(); //跳过当前位置向后的空格
public void moveForward(int step); //位置向前移动step步
public boolean isEnd(); //判断是否读到字符串末尾
public boolean isStartWithChar(char c); //判断是否以c字符开头
public boolean isStartWithString(String s); //判断是否以s字符串开头
...
这样的设计,减少了递归下降过程中代码的重复,增加了可读性,使思路更加明晰
ExpressionParser实现了上面描述的递归下降算法,不再赘述,复杂度如下
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
ExpressionParser.ExpressionParser(String) |
0.0 | 1.0 | 1.0 | 1.0 |
ExpressionParser.getConstant() |
0.0 | 1.0 | 1.0 | 1.0 |
ExpressionParser.getCos() |
18.0 | 8.0 | 10.0 | 11.0 |
ExpressionParser.getMultiplicationSign() |
3.0 | 3.0 | 3.0 | 3.0 |
ExpressionParser.getOperator() |
4.0 | 4.0 | 4.0 | 4.0 |
ExpressionParser.getPoly() |
1.0 | 1.0 | 2.0 | 2.0 |
ExpressionParser.getPolyUnit() |
2.0 | 2.0 | 2.0 | 2.0 |
ExpressionParser.getPower() |
12.0 | 5.0 | 7.0 | 8.0 |
ExpressionParser.getSignedInteger() |
6.0 | 3.0 | 3.0 | 5.0 |
ExpressionParser.getSin() |
18.0 | 8.0 | 10.0 | 11.0 |
ExpressionParser.getTerm() |
3.0 | 1.0 | 4.0 | 4.0 |
ExpressionParser.getUnit() |
7.0 | 6.0 | 8.0 | 8.0 |
ExpressionParser.isEnd() |
0.0 | 1.0 | 1.0 | 1.0 |
| Total | 74.0 | 44.0 | 56.0 | 61.0 |
| Average | 5.6923076923076925 | 3.3846153846153846 | 4.3076923076923075 | 4.6923076923076925 |
由于需要分析各种不同类型的格式错误,因此不可避免的在某些方法中的判断语句过多
InputWongFormatException自定义的异常类,继承自Exception,用于在检测到输入格式错误时抛出异常
虽然只需要输出一个WONG FORMAT!!!,但也要符合面向对象的设计,Java的抛出异常机制非常实用,建议好好学习一下
类内虽然只有几行,但也是符合面向对象的代码:
private String exceptionInfor;
public InputWrongFormatException() { //在构造函数中初始化,这样方便应对未来多变的需求
exceptionInfor = "WRONG FORMAT!";
}
public String getExceptionInfor() { //不要将错误信息设置为public,而是留下相应的方法
return exceptionInfor; //这样外部只需要System.out.println(e.getExceptionInfor());即可
}
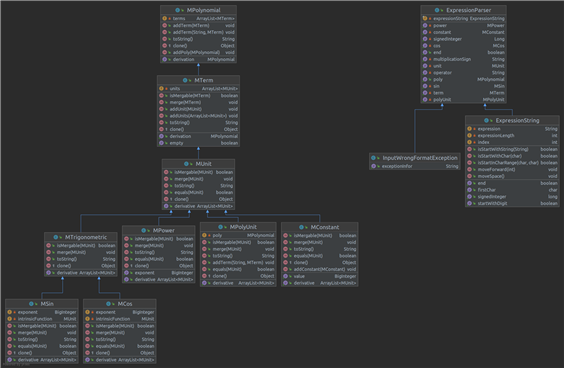
为了放置和内置库冲突,在自定义的类之前加一个M表示My
MPolynolmial(多项式)MPolynomial类代表了一整个表达式
其基本形式是许多项的和,因此也可以看成是一个项的累加类
成员只有一个项的ArrayList
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
MPolynomial.addPoly(MPolynomial) |
8.0 | 4.0 | 5.0 | 5.0 |
MPolynomial.addTerm(MTerm) |
4.0 | 3.0 | 4.0 | 4.0 |
MPolynomial.addTerm(String,MTerm) |
2.0 | 1.0 | 3.0 | 3.0 |
MPolynomial.clone() |
2.0 | 1.0 | 3.0 | 3.0 |
MPolynomial.getDerivation() |
1.0 | 1.0 | 2.0 | 2.0 |
MPolynomial.MPolynomial() |
0.0 | 1.0 | 1.0 | 1.0 |
MPolynomial.toString() |
6.0 | 1.0 | 4.0 | 6.0 |
| Total | 23.0 | 12.0 | 22.0 | 24.0 |
| Average | 3.2857142857142856 | 1.7142857142857142 | 3.142857142857143 | 3.4285714285714284 |
类的主要方法如上,可以看到每一个方法都较为简短
MPoly中的几个方法说明面向对象的思想getDerivation()由于MPoly是一个累加类,因此他的导数就等于各个项的导数的和,因此函数体为
MPolynomial poly = new MPolynomial();
for (MTerm term : terms) {
MPolynomial derivation = term.getDerivation();
poly.addPoly(derivation);
}
return poly;
MPoly类不会考虑如何得到一个项的导数,他会把这项任务交给一个MTerm(项)去做,MPoly只管跟一个MTerm要他的导数
需要注意的是:MPoly的导数依旧是一个MPoly,因为\((a+b)‘=a‘+b‘\)依旧是一个多项式,只有在Main函数的最后输出时,再调用MPoly的toString()方法获得字符串形式
toString()到得到MPoly的字符串形式,只需要获得每一项的的字符串,并拼接起来即可
其中有一些小小的细节需要考虑,比如项的第一个字符需要是正负号
因此函数体为
String ans = "";
for (MTerm term : terms) { //最重要的6行代码
String next = term.toString();
if (!next.equals("+0") && !next.equals("0")) { //小优化:如果Term是0,则跳过
ans += next;
}
}
if (ans.equals("")) { //如果到最后还是0,则ans为“0”
ans = "0";
}
if (ans.charAt(0) == ‘+‘) { //如果第一个字符为‘+‘,则删掉
ans = ans.substring(1);
}
return ans;
addPoly()在getDerivation()中,我们得到的每一个MTerm的导数都是一个MPoly,每一次需要将新的多项式加到已有的多项式中,因此需要一个addPoly(MPolynomial newPoly)方法
我们需要遍历已有的MTerm,每一次再遍历新的newPoly的所有项,如果两个项能够合并,就合并他们(这其实是一个优化过程,也可以不判断直接加到MTerm的ArrayList中),因此函数体为
for (MTerm newTerm : poly.terms) {
boolean foundMergableTerm = false; //记录是否找到了一个可以合并的项
for (MTerm term : terms) {
if (term.isMergable(newTerm)) {
term.merge(newTerm);
foundMergableTerm = true;
break;
}
}
if (!foundMergableTerm) {
terms.add(newTerm);
}
}
相信这几个例子就能够展现面向过程的魅力了。一个类不会过多的考虑除了自己意外的细节,把能交给别人做的事情都交给别人,自己只管提出需求。这样写代码会思路清晰,维护简单且可读性好
MTerm(项)MTerm类代表了一个类
其基本形式是许多因子的成绩,因此也可以看成是一个因子的累乘类
成员只有一个因子的ArrayList
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
MTerm.addUnit(MUnit) |
4.0 | 3.0 | 4.0 | 4.0 |
MTerm.addUnits(ArrayList) |
1.0 | 1.0 | 2.0 | 2.0 |
MTerm.clone() |
2.0 | 1.0 | 3.0 | 3.0 |
MTerm.getDerivation() |
6.0 | 1.0 | 4.0 | 4.0 |
MTerm.isEmpty() |
0.0 | 1.0 | 1.0 | 1.0 |
MTerm.isMergable(MTerm) |
16.0 | 4.0 | 5.0 | 8.0 |
MTerm.merge(MTerm) |
10.0 | 6.0 | 2.0 | 6.0 |
MTerm.MTerm() |
0.0 | 1.0 | 1.0 | 1.0 |
MTerm.toString() |
9.0 | 3.0 | 4.0 | 8.0 |
| Total | 48.0 | 21.0 | 26.0 | 37.0 |
| Average | 5.333333333333333 | 2.3333333333333335 | 2.888888888888889 | 4.111111111111111 |
绝大部分方法依然比较简短,只有在判断两个项是否需要合并时较为复杂,不具有普遍意义
具体的实现就不再赘述,与MPolynomial的思想是完全相同的,将更基础的事交给底下的MUnit(因子)去做
MUnit(因子)MUnit是所有因子的父类,可以定义为一个抽象类或者是借口,因为我们不需要创建一个MUnit对象,只会创建如cos,sin,x**2等因子对象
MUnit规定子类需要实现的方法有:
public ArrayList<Munit> getDerivative(); //计算因子自己的导数
public boolean isMergale(MUnit newUnit); //判断自己能否与另一个因子合并
public void merge(MUnit newUnit); //与另一个能够合并的因子合并
public String toString(); //返回自己的字符串形式
public boolean equals(Object o); //判断自己是否与另一个因子相等
public MUnit clone(); //将自己深层克隆一份
MConstant(常数因子)MPower(幂函数)幂函数主要由指数组成,我的设计中没有“变量”这一个概念,而是用幂函数来代替“变量”,其他的如\(sin(x)**2\)不是幂函数,而是三角函数,三角函数自己有一个指数
因此,如果要增加多变量求偏导数的需求,只需要更改MPower类的内容,增加成员“变量”,并修改求导、求字符串等函数即可
细节不再赘述,其复杂度如下。可以看到也较为简单
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
MPower.clone() |
0.0 | 1.0 | 1.0 | 1.0 |
MPower.equals(MUnit) |
1.0 | 1.0 | 2.0 | 2.0 |
MPower.getDerivative() |
0.0 | 1.0 | 1.0 | 1.0 |
MPower.getExponent() |
0.0 | 1.0 | 1.0 | 1.0 |
MPower.isMergable(MUnit) |
0.0 | 1.0 | 1.0 | 1.0 |
MPower.merge(MUnit) |
0.0 | 1.0 | 1.0 | 1.0 |
MPower.MPower(BigInteger) |
0.0 | 1.0 | 1.0 | 1.0 |
MPower.MPower(BigInteger,MUnit) |
0.0 | 1.0 | 1.0 | 1.0 |
MPower.MPower(String) |
0.0 | 1.0 | 1.0 | 1.0 |
MPower.toString() |
3.0 | 1.0 | 3.0 | 3.0 |
| Total | 4.0 | 10.0 | 13.0 | 13.0 |
| Average | 0.4 | 1.0 | 1.3 | 1.3 |
MTrigonometric(三角函数)MCos和MSin的父类,只是为了增加程序的扩展性,在这三次作业中没起到任何作用,也没有任何有意义的、与MUnit不重复的方法MSin(sin函数) MCos(cos函数)一个BigInteger成员作为指数,一个MUnit成员作为内函数(只有第三次作业从单独的x变为一个因子)
其余不再赘述,复杂度如下
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
MSin.clone() |
1.0 | 1.0 | 2.0 | 2.0 |
MSin.equals(MUnit) |
1.0 | 1.0 | 3.0 | 3.0 |
MSin.getDerivative() |
1.0 | 1.0 | 2.0 | 2.0 |
MSin.isMergable(MUnit) |
1.0 | 1.0 | 2.0 | 2.0 |
MSin.merge(MUnit) |
0.0 | 1.0 | 1.0 | 1.0 |
MSin.MSin() |
0.0 | 1.0 | 1.0 | 1.0 |
MSin.MSin(BigInteger,MUnit) |
0.0 | 1.0 | 1.0 | 1.0 |
MSin.toString() |
3.0 | 1.0 | 3.0 | 3.0 |
| Total | 7.0 | 8.0 | 15.0 | 15.0 |
| Average | 0.875 | 1.0 | 1.875 | 1.875 |
MPolyUnit(表达式因子)MPolyUnit只有一个MPolynomial成员,两者的本质区别就在于,MPolyUnit继承自MUnit,以及比MPolynomial在toString()中两侧套了一组括号,其余方法均直接调用MPolynomial的同名方法面向对象编程的一大特点就是——bug少,而且容易找到。编写内核代码的过程十分顺畅,且几乎不产生bug,即使有,也很快就能找得出。
我认为,原因就在于面向对象编程时,会将一个任务分解成一个个小任务,并且任务之间的耦合度比较低
比如说,我需要完成“表达式求导”这一项任务,那么一个MPoly需要做的就是以下几步:
- 创建一个新的表达式
- 遍历自己的每一项
- 获得每一项的导数
- 将获得的导数添加到新的表达式中
- 遍历完成,返回新的表达式
这五个步骤几乎不涉及到任何的细节问题,而是对任务做出规划,因此这一段代码出bug的概率极低
这样一层一层的将任务细化,最终只有很少部分的方法需要考虑细节问题,大大降低了bug的可能性
原文:https://www.cnblogs.com/beityluo/p/14587894.html