一、实验准备
1.图片采集,使用oppoR15手机拍摄集美大学的建筑物图像。(友情提示:因为用数组保存处理图片,所以要求图片大小要一致,并且,图片不能太大,几MB的跑不动,手机拍下来的图片像素太高,我用ps降低它的分辨率,将几MB级别的照片压缩到几十KB)
2.熟悉SIFT算法的原理,流程,SIFT算法所需要的函数在《Python计算机视觉编程》一书中有详细的记载,我将用到的函数保存到sift.py文件中,然后在后续实验代码中直接调用。
二、SIFT算法
1.SIFT算法简介
Sift算子是一种局部描述子,Sift特征匹配算法可以处理两幅图像之间发生平移、旋转、仿射变换情况下的匹配问题,具有很强的匹配能力。SIFT特征对于尺度、旋转和亮度都具有不变性,它的主要思想是在尺度空间寻找极值点,然后对极值点进行过滤,找出稳定的特征点。最后在每个稳定的特征点周围提取图像的局部特性,形成局部描述子并将其用在以后的匹配中,具有很强的健壮性。
2.SIFT算法流程
(1)检测兴趣点
(2)抽取稳定的关键点,为每个关键点指定一个或者多个方向,生成特征点描述子
(3)通过特征点的匹配建立图像间的对应关系
3.sift.py文件内容
from pylab import * from PIL import Image from numpy import * import os
检测兴趣点函数
def process_image(imagename, resultname, params="--edge-thresh 10 --peak-thresh 5"): """处理一幅图像,然后将结果保存在文件中""" if imagename[-3:] != ‘pgm‘: # 创建一个pgm文件 im = Image.open(imagename).convert(‘L‘) im.save(‘tmp.pgm‘) imagename = ‘tmp.pgm‘ cmmd = str("sift " + imagename + " --output=" + resultname + " " + params) os.system(cmmd) print(‘processed‘, imagename, ‘to‘, resultname) def read_features_from_file(filename): """读取特征值属性值,然后将其以矩阵形式返回""" f = loadtxt(filename) return f[:, :4], f[:, 4:] # 特征位置,描述子
def plot_features(im, locs, circle=False): """显示带有特征的图像 输入:im(数组图像),locs(每个特征的行、列、尺度和方向角度)""" def draw_circle(c,r): t = arange(0,1.01,.01)*2*pi x = r*cos(t) + c[0] y = r*sin(t) + c[1] plot(x,y,‘b‘,linewidth=2) imshow(im) if circle: for p in locs: draw_circle(p[:2],p[2]) else: plot(locs[:,0],locs[:,1],‘ob‘) axis(‘off‘) return
匹配描述子
def match(desc1, desc2): """对于第一幅图像的每个描述子,选取其在第二幅图像中的匹配 输入:desc1(第一幅图像中的描述子),desc2(第二幅图像中的描述子)""" desc1 = array([d/linalg.norm(d) for d in desc1]) desc2 = array([d/linalg.norm(d) for d in desc2]) dist_ratio = 0.6 desc1_size = desc1.shape matchscores = zeros((desc1_size[0],1), ‘int‘) desc2t = desc2.T #预先计算矩阵转置 for i in range(desc1_size[0]): dotprods = dot(desc1[i,:], desc2t) #向量点乘 dotprods = 0.9999*dotprods # 反余弦和反排序,返回第二幅图像中特征的索引 index = argsort(arccos(dotprods)) # 检查最近邻的角度是否小于dist_ratio乘以第二近邻的角度 if arccos(dotprods)[index[0]] < dist_ratio * arccos(dotprods)[index[1]]: matchscores[i] = int(index[0]) return matchscores
为了进一步增加匹配的稳健性,我们可以反过来执行一次该操作,进行双向匹配,函数如下:
def match_twosided(desc1,decs2): """双向对称版本的match""" matches_12 = match(desc1, decs2) matches_21 = match(decs2, desc1) ndx_12 = matches_12.nonzero()[0] # 去除不对称匹配 for n in ndx_12: if matches_21[int(matches_12[n])] != n: matches_12[n] = 0 return matches_12
def plot_matches(im1, im2, locs1, locs2, matchscores, show_below=True): """显示一幅带有连接匹配之间连线的图片 输入:im1,im2(数组图像),locs1,locs2(特征位置),matchscores(match的输出), show_below(如果图像应该显示再匹配下方)""" im3 = appendimages(im1,im2) if show_below: im3 = vstack((im3,im3)) imshow(im3) cols1 = im1.shape[1] for i in range(len(matchscores)): if matchscores[i] > 0: plot([locs1[i, 0], locs2[matchscores[i, 0], 0] + cols1], [locs1[i, 1], locs2[matchscores[i, 0], 1]], ‘c‘) axis(‘off‘)
三、实验内容
1.两幅图片的关键点提取和匹配:
from pylab import * from PIL import Image from numpy import * import os import sift import pydot im1_name = ‘jf1.jpg‘ im2_name = ‘jf2.jpg‘ im1 = array(Image.open(im1_name)) im2 = array(Image.open(im2_name)) sift.process_image(im1_name, ‘jf1.sift‘) sift.process_image(im2_name, ‘jf2.sift‘) l1,d1 = sift.read_features_from_file(‘jf1.sift‘) l2,d2 = sift.read_features_from_file(‘jf2.sift‘) figure() gray() subplot(221) imshow(Image.open(im1_name)) subplot(222) imshow(Image.open(im2_name)) subplot(223) sift.plot_features(im1, l1, circle=False) subplot(224) sift.plot_features(im2,l2,circle=False) matches = sift.match_twosided(d1, d2) print(‘{} matches‘.format(len(matches.nonzero()[0]))) figure() gray() sift.plot_matches(im1, im2, l1, l2, matches, show_below=True) show()
代码说明:
(1)调用process_image函数对图像进行特征点检测和提取,获得的描述子详细信息会保存在jf1.sift和jf2.sift文件中,文件中每一行表示一个兴趣点,前四个数值依次表示兴趣点的坐标、尺度和方向角度,后面紧接着是对应描述符的128维向量。
(2)调用sift.read_features_from_file函数读取特征属性值,l1,l2是特征位置的矩阵,d1,d2是描述子(128维向量)的矩阵
(3)调用plot_features函数画出特征点,plot_matches画出匹配特征点之间的连线
2.实验结果
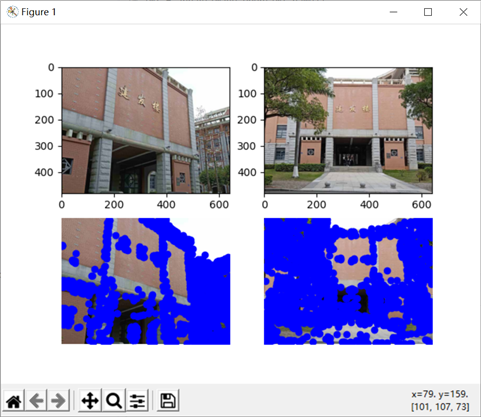
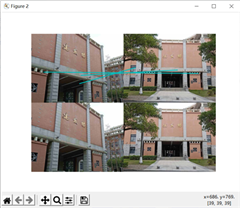
实验结果分析:
左图显示的是第一行两张图片的特征点提取,两张图片取自同一座教学楼,但是拍摄的角度和远近不同,右图结果显示用sift匹配算法匹配的结果是只有三个特征点匹配,并且,仔细一看还发现其中两个点虽然连线,但是并不是同一个点。说好的sift具有尺度不变性的呢?我个人的理解是(不知道对不对),sift的匹配准确度高是在于,空间尺度不变性,它通过高斯金字塔进行尺度变换,然后之所以具有旋转不变性是因为对特征点的位置方向描述是基于周围的像素的影响,是相对固定不变的,就好比,我在行驶的火车上,我相对火车外部环境是不断变化的,但是,我相对车内部环境是相对固定的,可以详细描述的,可能这个例子不是很合适,但是这是我的个人理解。所以,我觉得这两张图片之所以匹配度不高,主要是因为左图比较不完整,只有局部,而且建筑内部相似度也比较高。
2.图片匹配可视化
imlist = [‘jf1.jpg‘,‘jf2.jpg‘,‘jf3.jpg‘,‘jf4.jpg‘,‘dy1.jpg‘,‘dy2.jpg‘,‘sz.jpg‘] featlist = [‘jf1.sift‘,‘jf2.sift‘,‘jf3.sift‘,‘jf4.sift‘,‘dy1.sift‘,‘dy2.sift‘,‘sz.sift‘] for i in range(len(imlist)): sift.process_image(imlist[i], featlist[i]) nbr_images = len(imlist) matchscores = zeros((nbr_images, nbr_images)) for i in range(nbr_images): for j in range(i, nbr_images): print(‘comparing ‘, imlist[i], imlist[j]) l1, d1 = sift.read_features_from_file(featlist[i]) l2, d2 = sift.read_features_from_file(featlist[j]) matches = sift.match_twosided(d1, d2) nbr_matches = sum(matches > 0) print(‘number of matches = ‘, nbr_matches) matchscores[i, j] = nbr_matches for i in range(nbr_images): for j in range(i + 1, nbr_images): matchscores[j, i] = matchscores[i, j] threshold = 2 g = pydot.Dot(graph_type=‘graph‘) path = ‘D:\\JAVA\\eclipse_all_space\\eclipse\\workspace\\analySY\\‘ for i in range(nbr_images): for j in range(i + 1, nbr_images): if matchscores[i, j] > threshold: im = Image.open(imlist[i]) im.thumbnail((100, 100)) filename = str(i) + ‘.png‘ im.save(filename) g.add_node(pydot.Node(str(i), fontcolor=‘transparent‘, shape=‘rectangle‘, image=path+filename)) im = Image.open(imlist[j]) im.thumbnail((100, 100)) filename = str(j) + ‘.png‘ im.save(filename) g.add_node(pydot.Node(str(j), fontcolor=‘transparent‘, shape=‘rectangle‘, image=path+filename)) g.add_edge(pydot.Edge(str(i), str(j))) g.write_jpg(‘jf.png‘) axis(‘off‘) imshow(Image.open(‘jf.png‘)) show()
代码说明:
(1)imlist数组保存的是要匹配的图片的名字,featlist数组保存经过图片sift算法提取的描述子
(2)需要安装Graphviz和pydot,然后用pydot显示图片连接
(3)思路是:设置一个阈值,将两两图片的描述子进行匹配,匹配的描述子个数如果大于阈值,就认为这两张图片有联系,将两张图片用线连接,上面代码设置阈值为2。
实验结果:
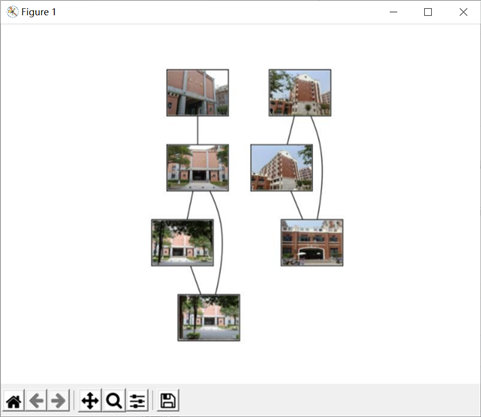
实验结果分析:
左边四张图都是建发楼的不同角度拍摄的图片,最上面的那张图片与其他图片的匹配度比较低,我觉得是因为下面三张图片的周围环境比较相似,角度也相似,而上面的那张图片比较局部化导致的。但是,右边的三张图,都是道远楼的照片,最下面的那张图片是大门,虽然与上面两张图的建筑连在一起,但是差别较大,只在上面两张图中露出一个小角落,却能匹配上,我觉得是阈值设置太低导致的。
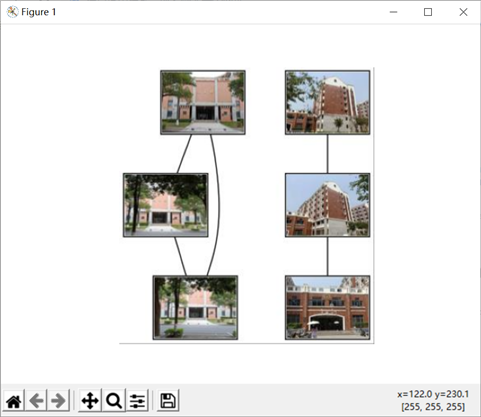
于是我将阈值改成了10,结果如下:
原文:https://www.cnblogs.com/dotime/p/14589366.html