本单元作为OO作为面对对象思想的引入,目的在于初步利用面对对象设计实现多项式求导。由于第一周缺乏对于可扩展性的追求,引来了后期重构的巨大麻烦,以致于最后都没有完全实现递归下降分析处理。
1.第一次作业
| 类 | 代码行数 | 属性个数 | 方法个数 |
|---|---|---|---|
| Polynomial | 102.0 | 2.0 | 5.0 |
| Mainclass | 29.0 | 0.0 | 1.0 |
| Total | 131.0 | 2.0 | 6.0 |
| Average | 65.5 | 1.0 | 3.0 |
| 方法 | 代码行数 | 循环嵌套 | 条件嵌套 | 认知复杂 | 基本复杂 | 设计复杂 | 圈复杂 |
|---|---|---|---|---|---|---|---|
| Polynomial.toTerm(BigInteger,BigInteger) | 16.0 | 0.0 | 0.0 | 32.0 | 1.0 | 10.0 | 12.0 |
| Polynomial.toString() | 18.0 | 1.0 | 1.0 | 6.0 | 1.0 | 4.0 | 5.0 |
| Polynomial.Polynomial(int) | 4.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Polynomial.parseStr(String) | 39.0 | 1.0 | 2.0 | 72.0 | 1.0 | 23.0 | 23.0 |
| Polynomial.isPos(String) | 5.0 | 0.0 | 0.0 | 2.0 | 1.0 | 4.0 | 5.0 |
| Polynomial.isNeg(String) | 5.0 | 0.0 | 0.0 | 2.0 | 1.0 | 4.0 | 5.0 |
| Polynomial.deriPoly() | 11.0 | 1.0 | 1.0 | 3.0 | 1.0 | 3.0 | 3.0 |
| Mainclass.main(String[]) | 27.0 | 1.0 | 1.0 | 5.0 | 1.0 | 4.0 | 4.0 |
| Total | 125.0 | 122.0 | 8.0 | 53.0 | 58.0 | ||
| Average | 15.625 | 0.5 | 0.625 | 15.25 | 1.0 | 6.625 | 7.25 |
分析
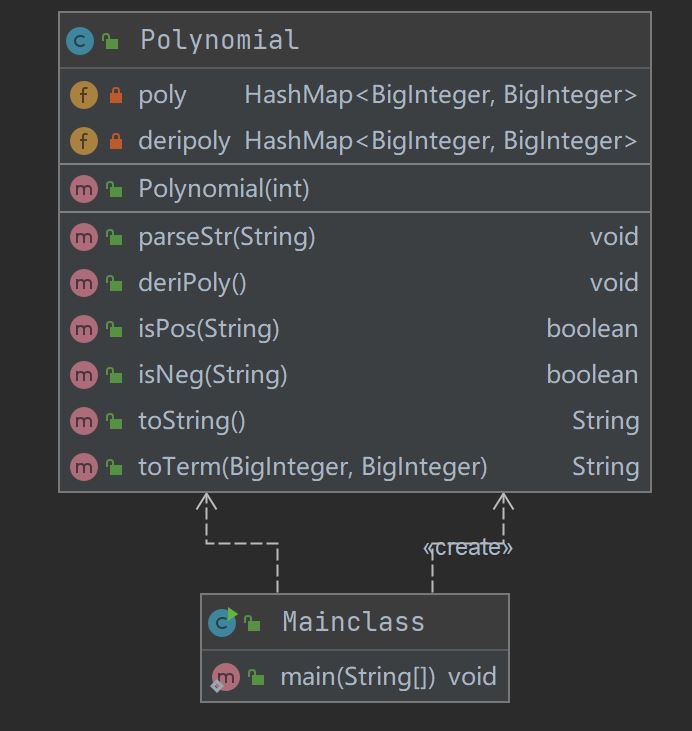
由于输入比较简单,用正则分离各项后用HashMap存储系数和指数,以非常短的行数实现。没有着重考虑用面对对象和递归下降实现,将多项式分析、求导、输出耦合在一个方法中,可以说是面对该次作业的编程。这导致parseStr(分析、求导全部耦合)的复杂度和行数远超其他方法。现在来看可以说是百害无一利的设计……仅有的一些好处就是极简代码+第一次作业中性能、互测无懈可击。
优化
由于直接HashMap直接存储系数,故直接利用相同指数合并,基本达到了最大性能。
2.第二次作业
| 类 | 代码行数 | 属性个数 | 方法个数 |
|---|---|---|---|
| AddExpression | 106.0 | 2.0 | 0.0 |
| Cons | 13.0 | 0.0 | 0.0 |
| Factor | 96.0 | 4.0 | 12.0 |
| Factory | 15.0 | 0.0 | 1.0 |
| MainClass | 11.0 | 0.0 | 1.0 |
| MultiplyTerm | 62.0 | 2.0 | 2.0 |
| TrigonCos | 77.0 | 1.0 | 0.0 |
| TrigonSin | 76.0 | 0.0 | 0.0 |
| Vari | 76.0 | 0.0 | 0.0 |
| Total | 532.0 | 9.0 | 16.0 |
| Average | 59.111111111111114 | 1.0 | 1.7777777777777777 |
| 方法 | 代码行数 | 循环嵌套 | 条件嵌套 | 认知复杂 | 基本复杂 | 设计复杂 | 圈复杂 |
|---|---|---|---|---|---|---|---|
| Vari.Vari(String) | 3.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Vari.toString() | 36.0 | 0.0 | 0.0 | 2.0 | 1.0 | 1.0 | 8.0 |
| Vari.todifferString() | 35.0 | 0.0 | 0.0 | 2.0 | 1.0 | 1.0 | 8.0 |
| TrigonSin.TrigonSin(String) | 3.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| TrigonSin.toString() | 36.0 | 0.0 | 0.0 | 2.0 | 1.0 | 1.0 | 8.0 |
| TrigonSin.todifferString() | 35.0 | 0.0 | 0.0 | 2.0 | 1.0 | 1.0 | 8.0 |
| TrigonCos.TrigonCos(String) | 3.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| TrigonCos.toString() | 36.0 | 0.0 | 0.0 | 2.0 | 1.0 | 1.0 | 8.0 |
| TrigonCos.todifferString() | 35.0 | 0.0 | 0.0 | 2.0 | 1.0 | 1.0 | 8.0 |
| MultiplyTerm.toString() | 11.0 | 1.0 | 1.0 | 3.0 | 3.0 | 2.0 | 3.0 |
| MultiplyTerm.todifferString() | 24.0 | 2.0 | 1.0 | 12.0 | 4.0 | 6.0 | 7.0 |
| MultiplyTerm.MultiplyTerm(String) | 18.0 | 1.0 | 2.0 | 12.0 | 1.0 | 8.0 | 8.0 |
| MultiplyTerm.differentiate() | 5.0 | 1.0 | 0.0 | 1.0 | 1.0 | 2.0 | 2.0 |
| MainClass.main(String[]) | 9.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Factory.getFactor(String) | 13.0 | 0.0 | 1.0 | 5.0 | 5.0 | 4.0 | 5.0 |
| Factor.todifferString() | 3.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.setIndex(BigInteger) | 3.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.setDerindex(BigInteger) | 3.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.setDericoef(BigInteger) | 3.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.setCoef(BigInteger) | 3.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.optimizationIndex(BigInteger) | 9.0 | 0.0 | 1.0 | 3.0 | 3.0 | 2.0 | 3.0 |
| Factor.optimizationCoef(BigInteger) | 11.0 | 0.0 | 1.0 | 4.0 | 4.0 | 3.0 | 4.0 |
| Factor.hashCode() | 4.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.getIndex() | 3.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.getDerindex() | 3.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.getDericoef() | 3.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.getCoef() | 3.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.Factor(String) | 16.0 | 0.0 | 2.0 | 9.0 | 1.0 | 4.0 | 5.0 |
| Factor.equals(Object) | 14.0 | 0.0 | 1.0 | 4.0 | 3.0 | 5.0 | 7.0 |
| Factor.differentiate() | 9.0 | 0.0 | 1.0 | 2.0 | 1.0 | 2.0 | 2.0 |
| Cons.toString() | 3.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Cons.todifferString() | 3.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Cons.Cons(String) | 5.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| AddExpression.toString() | 14.0 | 1.0 | 1.0 | 4.0 | 1.0 | 3.0 | 3.0 |
| AddExpression.todifferString() | 14.0 | 1.0 | 1.0 | 4.0 | 1.0 | 3.0 | 3.0 |
| AddExpression.hashCode() | 4.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| AddExpression.equals(Object) | 14.0 | 0.0 | 1.0 | 4.0 | 4.0 | 2.0 | 5.0 |
| AddExpression.differentiate() | 8.0 | 1.0 | 0.0 | 1.0 | 1.0 | 2.0 | 2.0 |
| AddExpression.AddExpression(String) | 48.0 | 1.0 | 3.0 | 32.0 | 5.0 | 18.0 | 20.0 |
| Total | 505.0 | 112.0 | 62.0 | 90.0 | 145.0 | ||
| Average | 12.948717948717949 | 0.23076923076923078 | 0.4358974358974359 | 2.871794871794872 | 1.5897435897435896 | 2.3076923076923075 | 3.717948717948718 |
分析
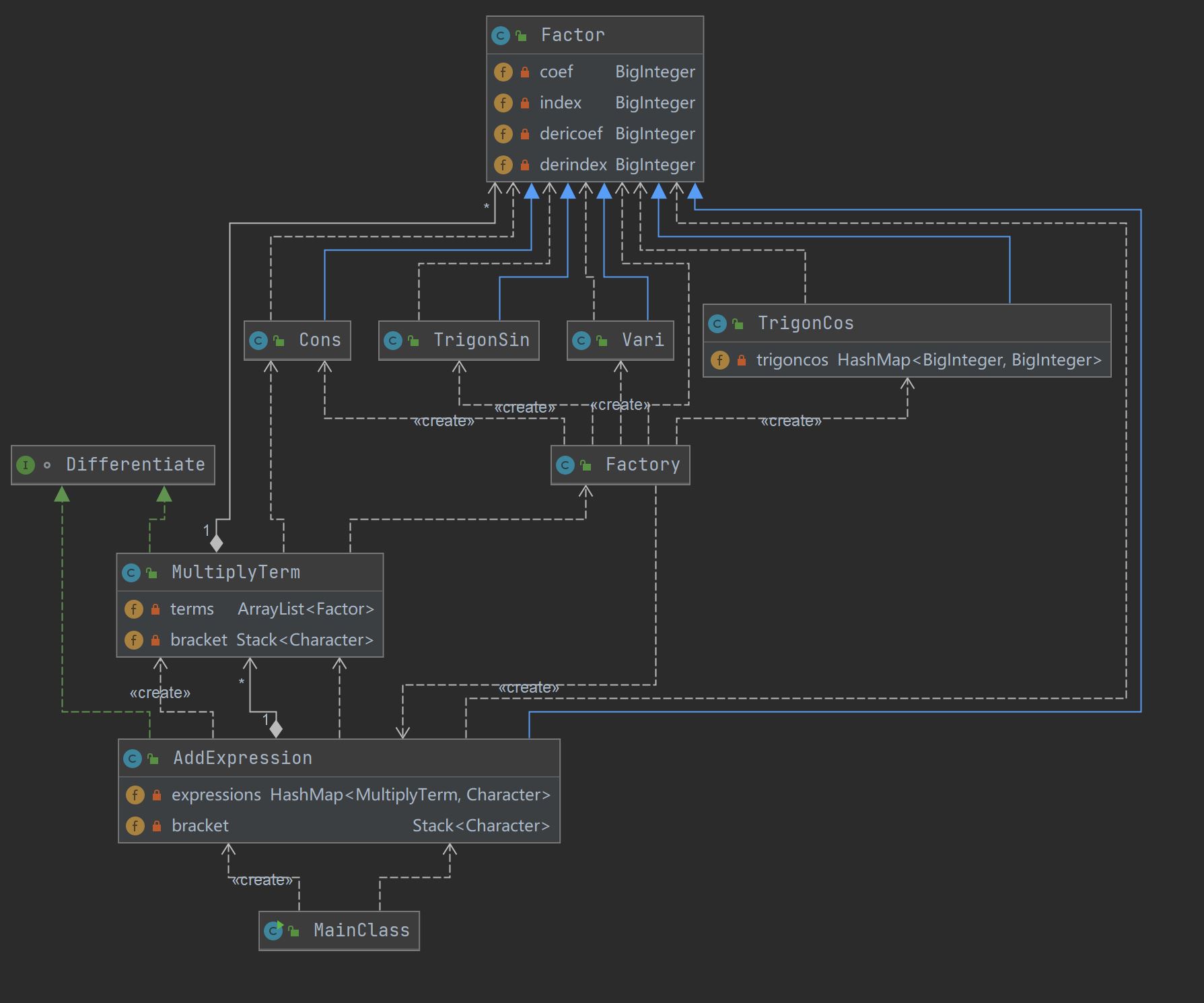
针对第二次作业的括号嵌套问题,作业一中的正则方法已经行不通了,只能重构。嵌套的分析使用了栈,并且嵌套调用表达式类和项类(因子可以是表达式,因子可以生成表达式对象)。使用工厂模式创建各种因子,编写toDiffString输出求导后表达式。代码量增长了4倍,其中因子类中创建了大量的set-get方法,复杂度集中在分析表达式输入AddExpression和求导输出toDiffString上。分离了求导、输出降低耦合度,这是第二次作业的优点。缺点是这种嵌套调用的方法使得求导比较复杂,这也是复杂度集中在求导输出上的原因。
优化
只做了系数为0、-1、1,指数为0、1特殊情况的输出处理。
3.第三次作业
| 类 | 代码行数 | 属性个数 | 方法个数 |
|---|---|---|---|
| AddExpression | 104.0 | 2.0 | 0.0 |
| CheckFormat | 137.0 | 1.0 | 3.0 |
| Cons | 13.0 | 0.0 | 0.0 |
| Factor | 119.0 | 5.0 | 12.0 |
| Factory | 15.0 | 0.0 | 1.0 |
| MainClass | 37.0 | 0.0 | 1.0 |
| MultiplyTerm | 77.0 | 3.0 | 2.0 |
| TrigonCos | 110.0 | 2.0 | 1.0 |
| TrigonSin | 111.0 | 2.0 | 1.0 |
| Vari | 76.0 | 0.0 | 0.0 |
| Total | 799.0 | 15.0 | 21.0 |
| Average | 79.9 | 1.5 | 2.1 |
| 方法 | 代码行数 | 循环嵌套 | 条件嵌套 | 认知复杂 | 基本复杂 | 设计复杂 | 圈复杂 |
|---|---|---|---|---|---|---|---|
| AddExpression.AddExpression(String) | 46.0 | 2.0 | 3.0 | 36.0 | 7.0 | 14.0 | 17.0 |
| AddExpression.differentiate() | 8.0 | 1.0 | 0.0 | 1.0 | 1.0 | 2.0 | 2.0 |
| AddExpression.equals(Object) | 14.0 | 0.0 | 1.0 | 4.0 | 4.0 | 2.0 | 5.0 |
| AddExpression.hashCode() | 4.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| AddExpression.todifferString() | 14.0 | 1.0 | 1.0 | 4.0 | 1.0 | 3.0 | 3.0 |
| AddExpression.toString() | 14.0 | 1.0 | 1.0 | 4.0 | 1.0 | 3.0 | 3.0 |
| CheckFormat.checkFormat(String) | 48.0 | 3.0 | 3.0 | 48.0 | 8.0 | 18.0 | 18.0 |
| CheckFormat.checkFormatOpt(String) | 26.0 | 2.0 | 5.0 | 46.0 | 9.0 | 14.0 | 16.0 |
| CheckFormat.checkOpt2(String) | 60.0 | 2.0 | 3.0 | 78.0 | 14.0 | 31.0 | 34.0 |
| Cons.Cons(String) | 5.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Cons.todifferString() | 3.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Cons.toString() | 3.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.differentiate() | 16.0 | 0.0 | 1.0 | 4.0 | 1.0 | 4.0 | 4.0 |
| Factor.equals(Object) | 15.0 | 0.0 | 1.0 | 4.0 | 3.0 | 6.0 | 8.0 |
| Factor.Factor(String) | 30.0 | 1.0 | 4.0 | 27.0 | 6.0 | 14.0 | 14.0 |
| Factor.getCoef() | 3.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.getDericoef() | 3.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.getDerindex() | 3.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.getIndex() | 3.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.hashCode() | 4.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.optimizationCoef(BigInteger) | 11.0 | 0.0 | 1.0 | 4.0 | 4.0 | 3.0 | 4.0 |
| Factor.optimizationIndex(BigInteger) | 9.0 | 0.0 | 1.0 | 3.0 | 3.0 | 2.0 | 3.0 |
| Factor.setCoef(BigInteger) | 3.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.setDericoef(BigInteger) | 3.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.setDerindex(BigInteger) | 3.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.setIndex(BigInteger) | 3.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.todifferString() | 3.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Factory.getFactor(String) | 13.0 | 0.0 | 1.0 | 5.0 | 5.0 | 4.0 | 5.0 |
| MainClass.main(String[]) | 35.0 | 1.0 | 5.0 | 28.0 | 1.0 | 12.0 | 12.0 |
| MultiplyTerm.differentiate() | 5.0 | 1.0 | 0.0 | 1.0 | 1.0 | 2.0 | 2.0 |
| MultiplyTerm.MultiplyTerm(String) | 36.0 | 1.0 | 2.0 | 18.0 | 3.0 | 10.0 | 12.0 |
| MultiplyTerm.todifferString() | 19.0 | 2.0 | 1.0 | 10.0 | 1.0 | 6.0 | 8.0 |
| MultiplyTerm.toString() | 12.0 | 1.0 | 1.0 | 3.0 | 3.0 | 2.0 | 3.0 |
| TrigonCos.getFactor() | 3.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| TrigonCos.todifferString() | 39.0 | 0.0 | 0.0 | 2.0 | 1.0 | 1.0 | 8.0 |
| TrigonCos.toString() | 37.0 | 0.0 | 0.0 | 2.0 | 1.0 | 1.0 | 8.0 |
| TrigonCos.TrigonCos(String) | 27.0 | 1.0 | 1.0 | 11.0 | 3.0 | 9.0 | 13.0 |
| TrigonSin.getFactor() | 3.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| TrigonSin.todifferString() | 40.0 | 0.0 | 0.0 | 2.0 | 1.0 | 1.0 | 8.0 |
| TrigonSin.toString() | 37.0 | 0.0 | 0.0 | 2.0 | 1.0 | 1.0 | 8.0 |
| TrigonSin.TrigonSin(String) | 27.0 | 1.0 | 1.0 | 11.0 | 3.0 | 9.0 | 13.0 |
| Vari.todifferString() | 35.0 | 0.0 | 0.0 | 2.0 | 1.0 | 1.0 | 8.0 |
| Vari.toString() | 36.0 | 0.0 | 0.0 | 2.0 | 1.0 | 1.0 | 8.0 |
| Vari.Vari(String) | 3.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Total | 764.0 | 362.0 | 105.0 | 193.0 | 264.0 | ||
| Average | 17.363636363636363 | 0.4772727272727273 | 0.8409090909090909 | 8.227272727272727 | 2.3863636363636362 | 4.386363636363637 | 6.0 |
分析
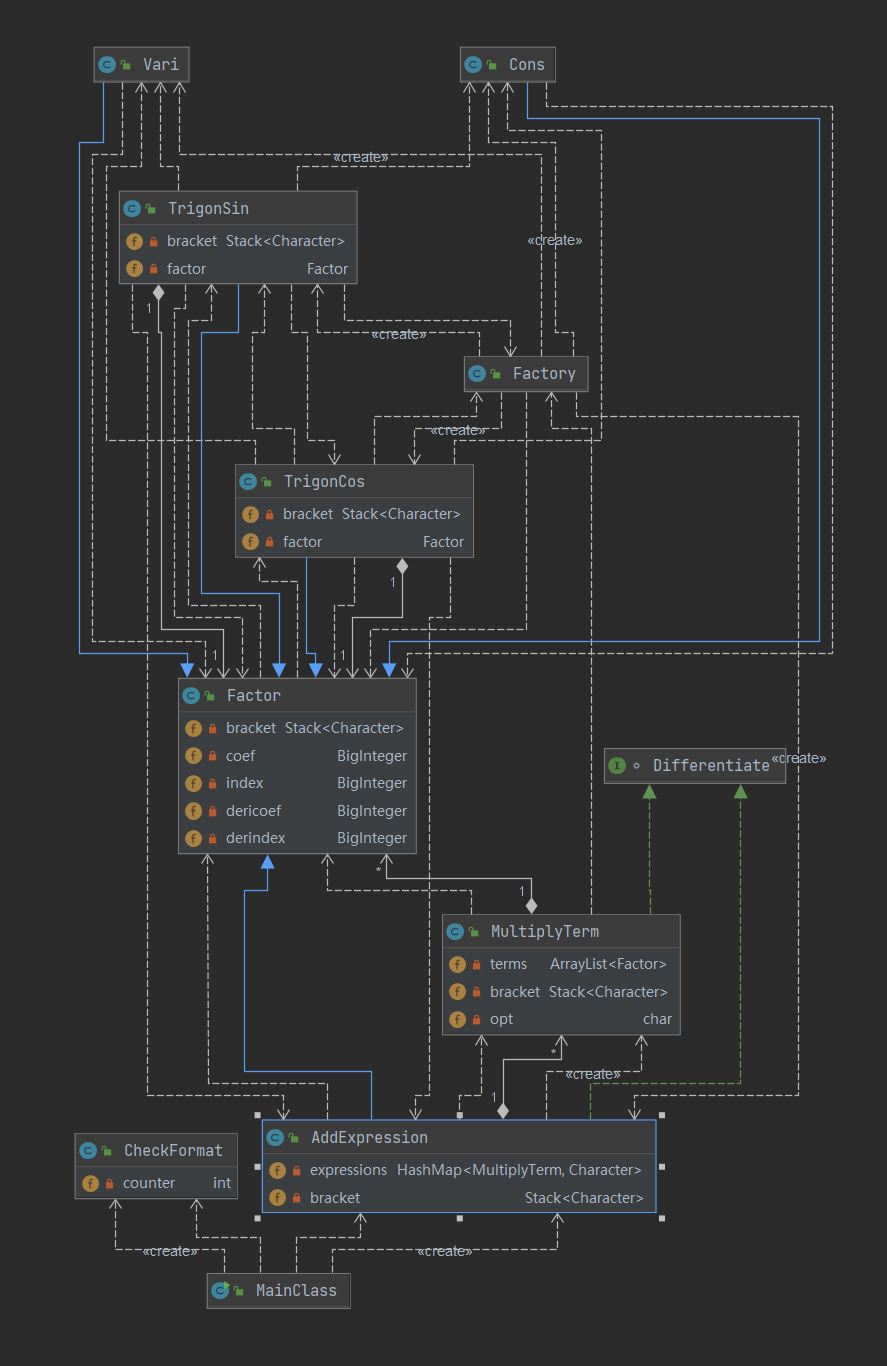
由于作业二未实现完备的递归下降分析,导致作业三检查WF必须新增一个CheckFormat类重新对输入进行检查,纯if-else结构使得类中方法条件嵌套、复杂度喜提所有方法第一。所幸嵌套结构依然可以实现复合求导,对三角函数因子类嵌套生成表达式因子。最后果然因为WF而非正确性错了两个强测点。这再次证明了在作业一时就注重可扩展性是多么重要。
==而没用equals()**)(())判断循环写错(重新开始时计数器是否需要增加)总结:最后一次明显是因为没有在分析多项式自动排除WF,用if-else特判会出现很多考虑不出来的情况。
sympy.diff())对比(simplify())。根据题目特别加大了嵌套深度,确实提高了hack出bug的几率。大规模重构是在第二次作业时,类图在上面已经放出就不再复制过来了。第一周过于粗暴地面对作业编程显然第二周将不可避免地推翻重构。针对面对对象的工厂模式、编写toDiffString()求导和输出分离解耦均是在第二周实现的。然而第三周依然经历了15h的痛苦编写检查WF类,归根到底是第二周的设计模式还不够彻底地递归下降。应该一个字符一个字符地生成检查而不是直接判断整个因子、项,传一个子串处理。后者再在检查WF时没法很好处理单个字符间的问题。
本单元在第一周的偷懒使得后面付出了成倍的代价,在下一单元应该提前设计好整个单元的程序结构,避免后面迭代带来的种种麻烦。同时希望之后在此基础上能多考虑一些性能的提升,因为后面的重构使得没多少时间去提升性能。
原文:https://www.cnblogs.com/NatsusakiYomi/p/14589404.html