
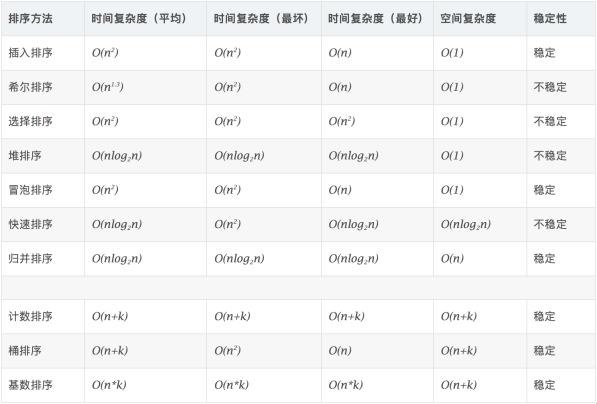
稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
不稳定:如果a原本在b的前面,而a=b,排序之后 a 可能会出现在 b 的后面。
时间复杂度:对排序数据的总的操作次数。反映当n变化时,操作次数呈现什么规律。
空间复杂度:是指算法在计算机内执行时所需存储空间的度量,它也是数据规模n的函数。
元素的移动次数与关键字的初始排列次序无关的是:基数排序
元素的比较次数与初始序列无关是:选择排序
算法的时间复杂度与初始序列无关的是:选择排序
假如我们要排序这几个数 6 1 2 7 9 3 4 5 10 8
我们都是先找左边第一个数用作一开始作比较的基数就是6,然后右边开始比较,假设左边的哨兵是i,右边的是j。
从j开始找到比6小的第一个数,停下来。在从左边的i开始找,找到第一个比6大的书停下来。最后是i停到了7,停在了5上面。
然后对两个哨兵进行交换


第一次交换结束
然后在按照刚刚的顺序,j在向左寻找,找到4比6小,i向右寻找,找到9比6大,之后交换

第二次结束
j在向左,找到3比6小,但是当i移动的时候两个哨兵相遇了,所以本次循环停止。停在3上面。最后在把3和基准数6交换之后完成。

以6为分界线,对左右边再次调用快速排序进行递归,算法完成

//快速排序(从小到大)
void quickSort(int left, int right, vector<int>& arr)
{
if(left >= right)
return;
int i, j, base, temp;
i = left, j = right;
base = arr[left]; //取最左边的数为基准数
while (i < j)
{
while (arr[j] >= base && i < j)
j--;
while (arr[i] <= base && i < j)
i++;
if(i < j)
{
temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
//基准数归位
arr[left] = arr[i];
arr[i] = base;
quickSort(left, i - 1, arr);//递归左边
quickSort(i + 1, right, arr);//递归右边
}
//快速排序(从大到小)
void quickSort(int left, int right, vector<int>& arr)
{
if(left >= right) //递归边界条件
return;
if(left < 0 || right >= arr.size())
{
cout << "error args! array bound." << endl;
return;
}//非法输入判断,防止数组越界
int i, j, base, temp;
i = left, j = right;
base = arr[left]; //取最左边的数为基准数
while (i < j)
{
while (arr[j] <= base && i < j)
j--;
while (arr[i] >= base && i < j)
i++;
if(i < j)
{
temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
//基准数归位
arr[left] = arr[i];
arr[i] = base;
quickSort(left, i - 1, arr);//递归左边
quickSort(i + 1, right, arr);//递归右边
}
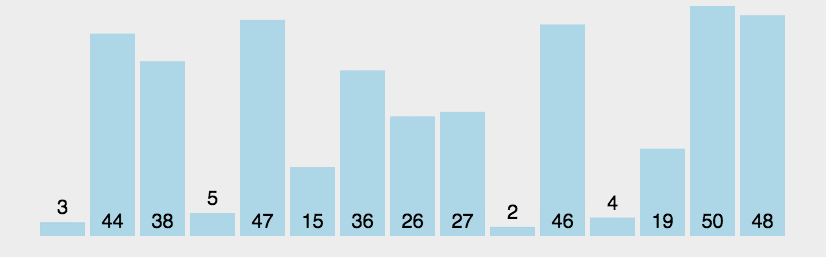
冒泡其实很好理解
冒泡就是把最大的东西放在后面(小到大)或把最小的放在后面(大到小)
方法就是在一次循环中遍历找到最大的数放到后面,找到一个比前面大的数就进行交换,
在从剩下的数中在重发刚刚的循环。完成
//冒泡排序
void BubbleSort(int* h, size_t len)
{
if(h==NULL) return;
if(len<=1) return;
int temp;
//i是次数,j是具体下标
for(int i=0;i<len-1;++i)
{
for(int j=0;j<len-1-i;++j)
{
if(h[j]>h[j+1])
{
temp = h[j];
h[j+1] = h[j];
h[j] = temp;
}
}
}
}
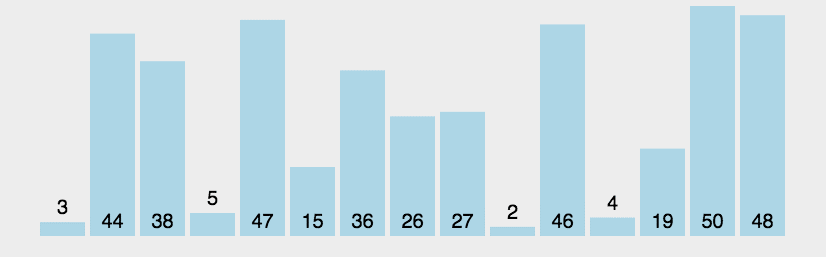
选择排序和冒泡的区别就是,他是最后交换,所以比冒泡做了优化,减少了交换次数。
方法就是用一个数做基准数,在一次循环中找到一个最大或最小的数,然后与最左或最右的数进行交换。
每次循环用相同方法。完成
//选择排序
void SelectionSort(int* h, size_t len)
{
if(h==NULL) return;
if(len<=1) return;
int minindex,i,j,temp;
//i是次数,也即排好的个数;j是继续排
for(i=0;i<len-1;++i)
{
minindex=i;
for(j=i+1;j<len;++j)
{
if(h[j]<h[minindex]) minindex=j;
}
temp = h[j];//最后进行交换
h[j+1] = h[j];
h[j] = temp;
}
}
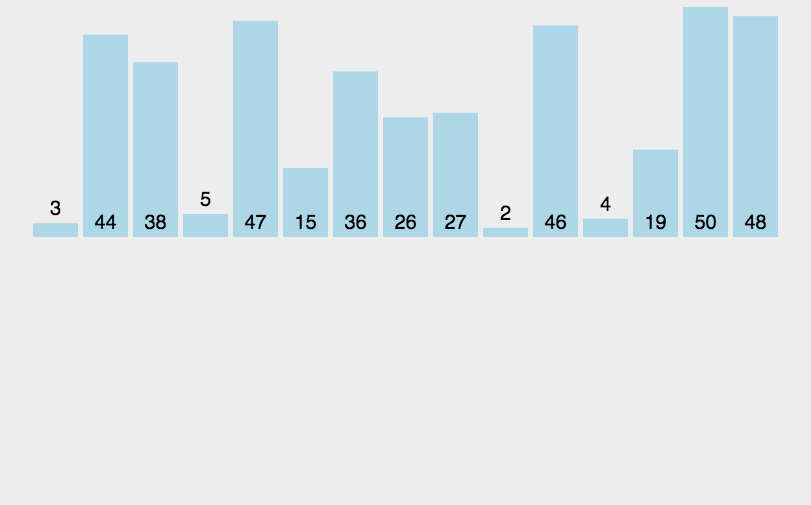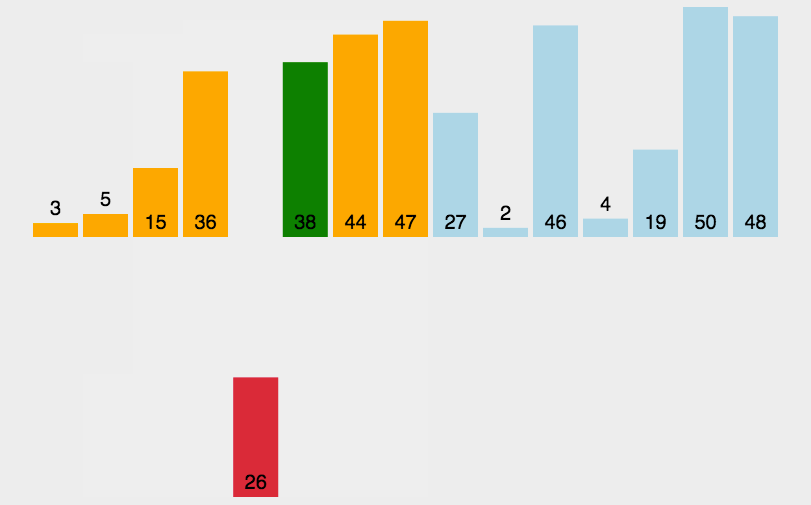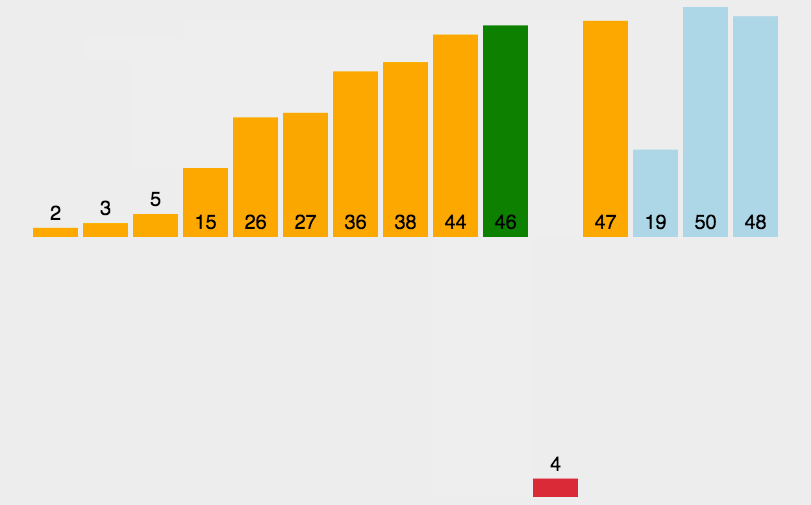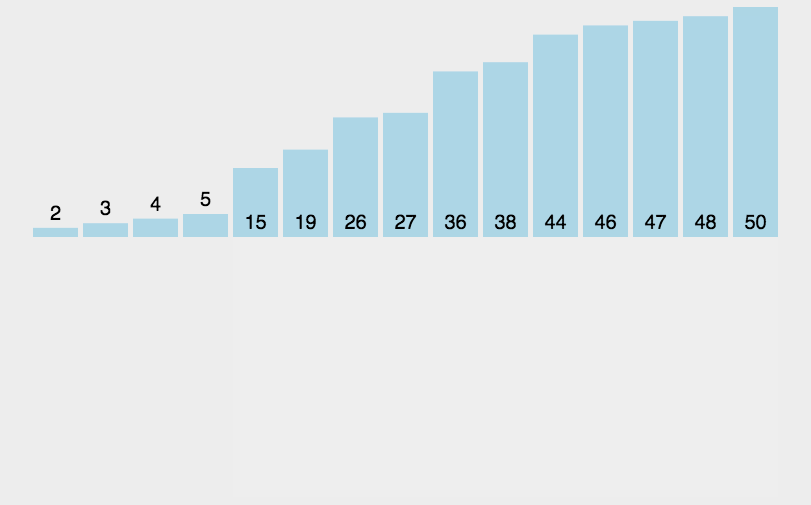
我的方法就是把要排列的数组看成两个数组
排序好的,和没有加入排序的。
每次从没有排序好的那一部分中取出一个数,和排序好的做比较,不符合要求就把数字向后移动一位留出空间,符合要求就进行插入操作。
void InsertSort(int a[], int len)
{
int i, j, k;
int tmp;
for (i = 1; i < len; i++) {
k = i; //待插入元素位置
tmp = a[k]; //先拿出来
for (j = i - 1; (j >= 0) && (a[j] > tmp); j--){
a[j + 1] = a[j]; //只要大,则元素后移
k = j; //记录移动的位置
}
a[k] = tmp; //元素插入
}
}
先把一个数组的所有的数字分成一半,一半,再一半,最后临时开辟的空间中排序合并。
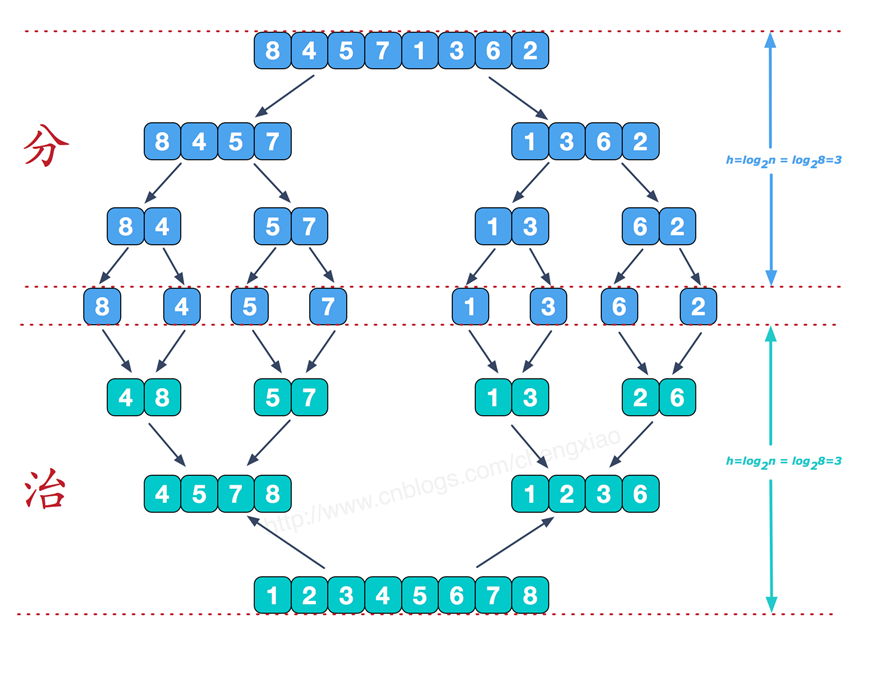
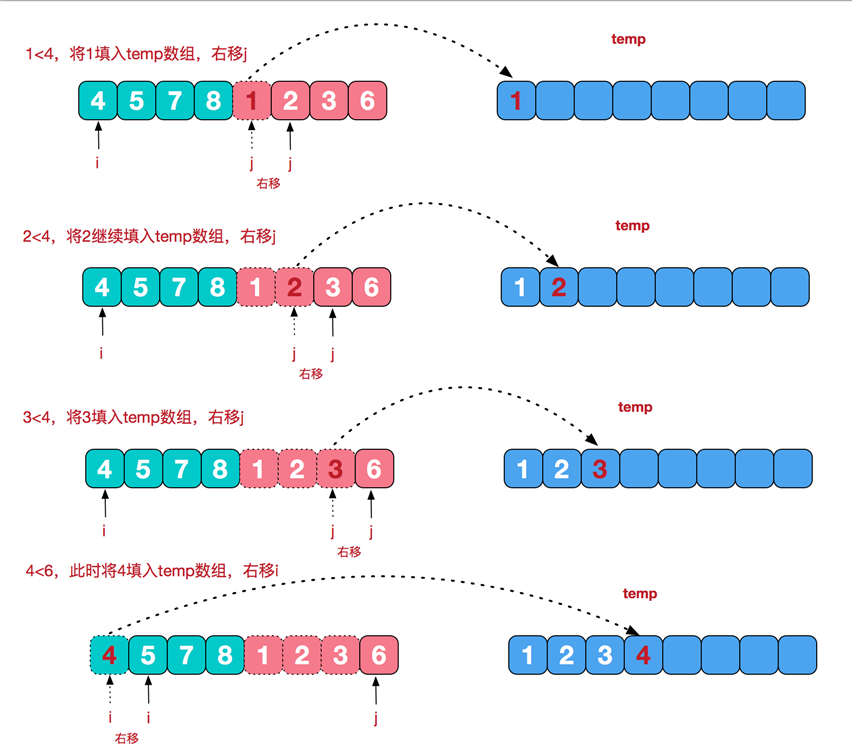
void MergeArray(int* arr, size_t left, size_t mid, size_t right, int* temp)
{
if(arr==NULL) return;
size_t i=left,j=mid+1,k=0;
while(i<=mid && j<=right)
{
if(arr[i]<=arr[j])
{
temp[k++]=arr[i++];
continue;
}
temp[k++]=arr[j++];
}
//将左边剩余元素填充进temp中
while(i<=mid)
temp[k++]=arr[i++];
//将右边子数组剩余部分填充到temp中
while(j<=right)
temp[k++]=arr[j++];
//将融合后的数据拷贝到原来的数据对应的子空间中
memcpy(&arr[left],temp,k*sizeof(int));
}
//归并排序
void MMergeSort(int* arr, size_t left, size_t right, int* temp)
{
if(left<right)
{
//分治
size_t mid=(left+right)/2;
MMergeSort(arr, left, mid, temp);
MMergeSort(arr, mid+1,right, temp);
MergeArray(arr,left, mid, right, temp);
}
}
//void MergeSort(int* h, size_t len)
//{
//if(h==NULL) return;
//if(len<=1) return;
//int* temp=(int*)malloc(len,sizeof(int));
//MMergeSort(h, 0, len-1, temp);
//memcpy(h,temp,sizeof(int)*len);
//free(temp);
//}
就是通过分组,再把分组里的书进行插入算法,这样比较的次数可能会减少。
分组一般是总数除2
void ShellSort(int a[], int len)
{
int i, j, k, tmp;
int gap = len;
do{
//gap的选择可以有多中方案,如gap = gap/2,这里使用的是业界统一实验平均情况最好的,收敛为1
gap = gap / 2;
for (i = gap; i < len; i += gap) //分成len/gap组
{
//每组使用插入排序
k = i;
tmp = a[k];
for (j = i - gap; (j >= 0) && (a[j] > tmp); j -= gap){
a[j + gap] = a[j];
k = j;
}
a[k] = tmp;
}
} while (gap > 1);
}
堆分为两类:
1、最大堆(大顶堆):堆的每个父节点都大于其孩子节点;
2、最小堆(小顶堆):堆的每个父节点都小于其孩子节点;
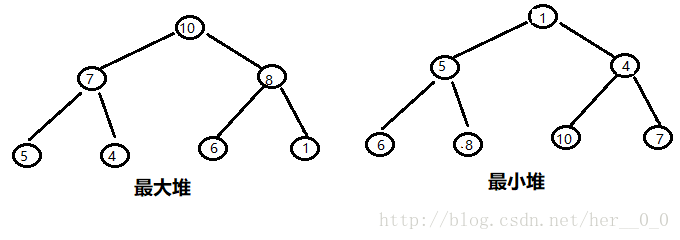
堆的存储:
一般都用数组来表示堆,i结点的父结点下标就为(i – 1) / 2。它的左右子结点下标分别为2 * i + 1和2 * i + 2。如下图所示:
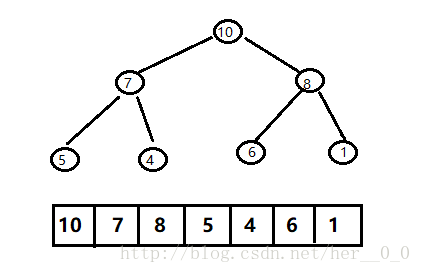

// 从小到大排序
void Down(int array[], int i, int n) { // 最后结果就是大顶堆
int temp;
int parent = i; // 父节点下标
int child = 2 * i + 1; // 子节点下标
while (child < n) {
if (child + 1 < n && array[child] < array[child + 1]) { // 判断子节点那个大,大的与父节点比较
child++;
}
if (array[parent] < array[child]) { // 判断父节点是否小于子节点
temp = array[parent];
array[parent] = array[child];
array[child] = temp; // 交换父节点和子节点
parent = child; // 子节点下标 赋给 父节点下标
}
child = child * 2 + 1; // 换行,比较下面的父节点和子节点
}
}
void BuildHeap(int array[], int size) {
for (int i = size / 2 - 1; i >= 0; i--) { // 倒数第二排开始, 创建大顶堆,必须从下往上比较
Down(array, i, size); // 否则有的不符合大顶堆定义
}
}
void HeapSort(int array[], int size) {
BuildHeap(array, size); // 初始化堆
for (int i = size - 1; i > 0; i--) {
temp = array[0];
array[0] = array[i];
array[i] = temp; // 交换顶点和第 i 个数据
// 因为只有array[0]改变,其它都符合大顶堆的定义,所以可以从上往下重新建立
Down(array, 0, i); // 重新建立大顶堆
}
}
https://www.cnblogs.com/chengxiao/p/6129630.html
https://blog.csdn.net/weixin_42109012/article/details/91668543
https://blog.csdn.net/qq_28584889/article/details/88136498
原文:https://www.cnblogs.com/sunnylinry/p/14590393.html