package learning.sort;
import java.lang.reflect.Method;
import java.util.*;
/**
* 排序算法集合
* 交换排序:冒泡排序、快速排序、三路切分快速排序
* 选择排序:简单选择排序、希尔排序
* 插入排序:直接插入排序、堆排序
* 归并排序
* 非比较排序:桶排序、计数排序、基数排序
*/
public class NumberSort {
/**
* 交换排序之冒泡排序:相邻的两个值相比较交换位置,把最大值交换到最右边,缩小范围重复上述步骤
*
* @param array 数组
*/
public static void bubbleSort(int[] array) {
// 是否已排序
boolean isSorted = false;
for (int i = 0; i < array.length - 1 && !isSorted; i++) {
// 默认本次交换后已经有序(如果不发生交换就已经有序了)
isSorted = true;
/*
从下标1开始依次与前一个数比较交换位置
1、为什么从下标1开始?
与前一个数比较不会存在越界问题
2、截止为什么是array.length - i?
每一次依次相邻比较并交换后会把最大值移到最右边,不用再参与排序
*/
for (int j = 1; j < array.length - i; j++) {
// 前一个数较大,交换位置
if (array[j - 1] > array[j]) {
swap(array, j - 1, j);
isSorted = false;
}
}
}
}
/**
* 交换排序之快速排序:通过一个切分元素将数组分为两个子数组,左子数组小于等于切分元素,右子数组大于等于切分元素。
* 通过上述规则不断切分左右子数组,直到各子区间只有一个数为止整个数组就有序了
*
* @param array 数组
*/
public static void quickSort(int[] array) {
quickSort(array, 0, array.length - 1);
}
/**
* 快排辅助方法
*
* @param array 数组
* @param left 左边界下标
* @param right 右边界下标
*/
private static void quickSort(int[] array, int left, int right) {
// 左边界大于等于右边界中断
if (left >= right) {
return;
}
// 左边开始下标
int i = left;
// 右边开始下标
int j = right;
// 基准数,这里取左边第一个数,且作为首个空位
int base = array[i];
// 左右边界向中间移动直到相遇
while (i < j) {
// 右边开始查找第一个小于基准数的下标
while (i < j && array[j] >= base) {
j--;
}
// 如果在右边找到小于基准数的值,放在数组左边空位(首个空位是基准数所在下标),下标i向右移动
if (i < j) {
// 右边形成一个新的空位array[j]
array[i++] = array[j];
}
// 左边开始查找第一个大于基准数的下标
while (i < j && array[i] <= base) {
i++;
}
// 如果在左边找到大于基准数的值,放在数组右边空位array[j],下标j向左移动
if (i < j) {
// 左边形成一个新的空位array[i]
array[j--] = array[i];
}
}
// 退出时i等于j,将基准数放入即可
array[j] = base;
// 左边子数组重复上述步骤
quickSort(array, left, i - 1);
// 右边子数组重复上述步骤
quickSort(array, i + 1, right);
}
/**
* 三向切分快速排序:将数组分为三部分:小于当前切分元素的部分、等于当前切分元素的部分、大于当前切分元素的部分,中间部分不再切分
* 好处在于若存在大量重复元素,重复元素总会位于中间部分,不再切分为更小数组,可以在线性时间内完成排序
*
* @param array 数组
*/
public static void threeWayQuickSort(int[] array) {
threeWayQuickSort(array, 0, array.length - 1);
}
/**
* 三向切分快排辅助方法
*
* @param array 数组
* @param left 左边界下标
* @param right 右边界下标
*/
private static void threeWayQuickSort(int[] array, int left, int right) {
// 左边界大于等于右边界中断
if (left >= right) {
return;
}
// 基准下标
int lt = left;
// 左子数组开始下标
int i = left + 1;
// 右子数组开始下标
int j = right;
// 基准数
int base = array[left];
// 遍历左右下标直到相遇(注意需要包含等于)
while (i <= j) {
// 小于基准数放入基准数所在下标,基准数下标右移,相当于放在其左边
if (array[i] < base) {
swap(array, lt++, i++);
// 大于基准数,和右边界数据交换位置,且缩小右边界,左边界下标不变重复第一步
} else if (array[i] > base) {
swap(array, i, j--);
// 等于基准数,左边界右移即可
} else {
i++;
}
}
// 小于基准数组成左子数组重复上述步骤
threeWayQuickSort(array, left, lt - 1);
// 大于基准数组成右子数组重复上述步骤
threeWayQuickSort(array, j + 1, right);
}
/**
* 选择排序之简单选择排序:每次选择最小值放在左边有序部分尾部
*
* @param array 数组
*/
public static void selectionSort(int[] array) {
// 从0~array.length - 2依次默认当前位置为最小值,在右边寻找真实最小值交换位置
for (int i = 0; i < array.length - 1; i++) {
// 默认当前下标i为最小值
int min = i;
// 在右边寻找真实最小值下标
for (int j = i + 1; j < array.length; j++) {
if (array[min] > array[j]) {
min = j;
}
}
// 如果最小下标不是当前默认位置,交换位置
if (i != min) {
swap(array, i, min);
}
}
}
/**
* 选择排序之堆排序:构建数组二叉堆(近似完全二叉树),利用父节点总是小于(大于)或等于任何一个子节点的特性,
* 根节点总是最大或最小值,摘除根节点加入有序序列,重新构建数组二叉堆重复上述步骤即可
*
* @param array 数组
*/
public static void heapSort(int[] array) {
int n = 2;
/*
构建二叉堆,从最后一个父节点开始
1、为什么最后一个父节点是array.length / 2 - 1?
最后一个元素下标i为array.length-1,根据父节点下标公式(i-1)/2得出,其父节点为(array.length-1-1)/2=array.length / 2 - 1
2、为什么从最后一个父节点开始?
二叉堆父节点总是大于(小于)或等于任何一个子节点。靠后的父节点也是子节点,从下层开始才能把较大(较小)节点上浮
*/
for (int i = array.length / n - 1; i >= 0; i--) {
buildHeap(array, array.length, i);
}
/*
二叉堆已构建,利用根节点总是最大(最小)的特性进行排序,把根节点交换到右侧后缩小数组范围重新构建二叉堆,重复上述步骤
i表示数组无序部分截止下标,交换到右侧的已经有序了,i缩小到0后整个数组就有序了
*/
for (int i = array.length - 1; i > 0; i--) {
// 交换根节点到最右侧
swap(array, 0, i);
// 交换后破坏了二叉堆结构,需要重新构建
buildHeap(array, i, 0);
}
}
/**
* 构建二叉堆(升序构建最大堆,降序构建最小堆)
*
* @param array 数组
* @param len 数组长度(构建二叉堆部分长度,排序时右侧部分逐渐有序,不参与堆结构构建)
* @param index 父节点下标
*/
private static void buildHeap(int[] array, int len, int index) {
// 父节点下标越界中断
while (index < len) {
// 左子节点,右子节点为left+1
int left = 2 * index + 1;
// 左子节点下标越界,证明没有子节点不需要调整位置
if (left >= len) {
break;
}
// 默认左子节点较大
int max = left;
// 与右子节点比较,得出最大值下标
if (left + 1 < len && array[left + 1] > array[max]) {
max = left + 1;
}
// 与父节点比较,若小于父节点不需要交换位置,中断循环
if (array[max] < array[index]) {
break;
}
// 若大于父节点交换位置
swap(array, max, index);
// 交换位置后,破坏了下层最大(小)堆结构,重置父节点进入下次循环
index = max;
}
}
/**
* 插入排序之直接插入排序:左边有序,从右边无序节点中依次选择节点,插入到左边合适的位置(从右向左扫描)
*
* @param array 数组
*/
public static void straightInsertSort(int[] array) {
// 左边默认一个元素且有序,右边无序元素从下标1开始
for (int i = 1; i < array.length; i++) {
// 与左边元素比较找到第一个小于的元素位置为止
for (int j = i; j > 0 && array[j - 1] > array[j]; j--) {
// 若左边的元素较大,交换位置,重复上述步骤找到合适位置
swap(array, j, j - 1);
}
}
}
/**
* 插入排序之希尔排序:本质上是多次的直接插入排序,通过步长构建新的子序列后进行直接插入排序,缩减步长重复上述步骤,
* 直到步长为1(步长为1时其实就是直接插入排序),好处在于直接插入排序在数据量小且有序的情况下效率最高
*
* @param array 数组
*/
public static void shellSort(int[] array) {
// 构建不断缩小的步长直到为1
int n = 2;
for (int gap = array.length / n; gap > 0; gap /= n) {
// 根据步长构建新的子序列进行直接插入排序
for (int i = gap; i < array.length; i += gap) {
for (int j = i; j >= gap && array[j - gap] > array[j]; j -= gap) {
swap(array, j - gap, j);
}
}
}
}
/**
* 归并排序:利用单个元素的有序性,反向合并两个有序数组
*
* @param array 数组
*/
public static void mergeSort(int[] array) {
mergeSort(array, 0, array.length - 1);
}
/**
* 把数组拆分为两个子数组分别排序后再合并,子数组的排序利用一个元素的数组是有序实现(不断拆分)
*
* @param array 数组
* @param left 左边界
* @param right 右边界
*/
private static void mergeSort(int[] array, int left, int right) {
// 左右边界未相遇,即只有一个元素(有序)
if (left < right) {
// 确认中间分界线
int mid = (left + right) / 2;
// 递归左子数组
mergeSort(array, left, mid);
// 递归右子数组
mergeSort(array, mid + 1, right);
// 合并左右有序数组
mergeSort(array, left, mid, right);
}
}
/**
* 合并左右有序数组
*
* @param array 数组
* @param left 左边界
* @param mid 子数组分界线
* @param right 右边界
*/
private static void mergeSort(int[] array, int left, int mid, int right) {
// 存放排序后数组
int[] temp = new int[right - left + 1];
// 左子数组开始下标
int i = left;
// 右子数组开始下标
int j = mid + 1;
// temp当前下标
int ix = 0;
// 从两个数组中选择较小的数放入temp中
while (i <= mid || j <= right) {
// 左子数组已经空了,直接把右子数组元素放入temp
if (i > mid) {
temp[ix++] = array[j++];
// 右子数组已经空了,直接把左子数组元素放入temp
} else if (j > right) {
temp[ix++] = array[i++];
// 左右子数组都为空,把较小的数组元素放入temp
} else if (array[i] < array[j]) {
temp[ix++] = array[i++];
} else {
temp[ix++] = array[j++];
}
}
// 把排序后值放入原数组
for (int n = left; n <= right; n++) {
array[n] = temp[n - left];
}
}
/**
* 桶排序:构建多个有序桶,按照一定规则把数据分到不同的桶里,桶内分别排序(直接插入排序),排序后按照桶顺序回放数据
*
* @param array 数组
*/
public static void bucketSort(int[] array) {
// 默认最大值
int maxLen = 1;
// 遍历原数组得出最大值、最小值
for (int value : array) {
int len = String.valueOf(value).length();
if (len > maxLen) {
maxLen = len;
}
}
// 创建一个桶集合,相同位数的放入同一个桶
List<LinkedList<Integer>> buckets = new ArrayList<>(maxLen);
// 初始化桶并加入到桶集合中,频繁插入选用链表结构LinkedList
for (int i = 0; i < maxLen; i++) {
buckets.add(new LinkedList<>());
}
// 遍历原数据均匀放入对应的桶中
for (int v : array) {
// 计算数据对应的桶,根据实际场景设计,保证数据可以均匀分布且桶之间数据有序
int ix = String.valueOf(v).length() - 1;
// 有序插入到桶中
bucketInsert(buckets.get(ix), v);
}
// 将桶中元素全部取出插入的原数组中
int ix = 0;
for (LinkedList<Integer> bucket : buckets) {
for (int v : bucket) {
array[ix++] = v;
}
}
}
/**
* 辅助桶排序:有序插入元素
*
* @param bucket 桶
* @param data 待插入数据
*/
private static void bucketInsert(List<Integer> bucket, int data) {
// 是否插入元素
boolean insertFlag = true;
// 使用迭代器遍历桶
ListIterator<Integer> it = bucket.listIterator();
while (it.hasNext()) {
// 如果待插入数据小于等于当前元素,就是需要插入的位置
if (data <= it.next()) {
// 迭代器位置偏移回上一个位置
it.previous();
// 位置偏移后插入元素,刚好就在本次比较元素之前
it.add(data);
// 元素已插入修改插入标志
insertFlag = false;
// 中断循环
break;
}
}
// 如果迭代过程没有插入说明待插入数据最大,插入到末尾
if (insertFlag) {
bucket.add(data);
}
}
/**
* 计数排序:本质上是一个特殊的桶排序,当桶的个数最大的时候,即相同的数一个桶,就是计数排序
* 创建一个长度为maxValue-minValue+1的数组计数,如下:
* 扫描一遍原始数组,以当前值- minValue 作为下标,将该下标的计数器增1
* 扫描一遍计数器数组,按顺序把值放回原数组
*
*
* @param array 数组
*/
public static void countingSort(int[] array) {
// 默认最小值
int min = array[0];
// 默认最大值
int max = array[0];
// 遍历原数组得出最大值、最小值
for (int i = 1; i < array.length; i++) {
if (array[i] < min) {
min = array[i];
} else if (array[i] > max) {
max = array[i];
}
}
// 定义一个计数数组
int[] count = new int[max - min + 1];
// 遍历原数组统计数据出现次数,注意下标需要用当前值- minValue,因为数组长度为max - min + 1
for (int v : array) {
count[v - min]++;
}
// 移动下标
int ix = 0;
// 遍历计数数组回放原数组
for (int i = 0; i < count.length; i++) {
// 出现次数,对应值为i + min
int cnt = count[i];
// 根据出现次数循环多次放入原数组
while (cnt-- > 0) {
array[ix++] = i + min;
}
}
}
/**
* 基数排序:构建有限的有序桶,把数据分类放入,更换分类指标重复上述步骤
* 例如:12 8 33 16,构建0~9号桶
* 第一步:低位作为指标分别放入2、3、6、8号桶,得出:12 33 16 8
* 第二步:高一位作为指标分别放入0、1、3号桶,得出:8 12 16 33,注意不要破坏低位的顺序
*
* @param array 数组
*/
public static void radixSort(int[] array) {
// 基数数组,数字0~9,长度10即可
int[] radix = new int[10];
// 排序后临时存放数组
int[] temp = new int[array.length];
// 不确定总共有多少位,用于统计信息判断是否中断循环
int cnt = 0;
// 用于去除低位的除数,1 10 100 ...
int m = 1;
// 从低位到高位进行排序
while (true) {
// 重置桶中上次统计的数据
for (int i = 0; i < radix.length; i++) {
radix[i] = 0;
}
// 统计当前位对应值出现的次数
for (int d : array) {
// 去除当前位右边的低位,m为除数,每迭代一次*10
int v = d / m;
// 统计数组中含有指定位数的数量
cnt = v > 1 ? cnt + 1 : cnt;
// 当前位对应值出现次数计数
radix[v % 10]++;
}
// 不存在指定位数的数,即没有更高的位了,中断循环
if (cnt == 0) {
break;
}
// 通过相邻的两个计数相加,得出基数对应的右边界(使用时需要减一)
for (int i = 1; i < radix.length; i++) {
radix[i] += radix[i - 1];
}
/*
把原数组中数据按照当前位依次放入临时数组中
1、相同位数据之间无序,不同位数据之间有序
2、必须倒序遍历原数组,可以保证高位排序后低位有序,因为是从右边界开始放入,例如 45 35 36 46,从右边取低位较大
*/
for (int i = array.length - 1; i >= 0; i--) {
// 当前位对应值
int ix = array[i] / m % 10;
// --radix[ix]为右边界下标,从右边界开始放入
temp[--radix[ix]] = array[i];
}
// 把部分有序的数据拷贝到原数组,进入高一位排序
for (int i = 0; i < temp.length; i++) {
array[i] = temp[i];
}
// 重置计数
cnt = 0;
// 高一位除数*10
m *= 10;
}
}
/**
* 数组指定位置交换值(一个数异或同一个数两次,结果还是那个数)
* 注意:下标i、j相同不能使用异或交换
*
* @param array 数组
* @param i 交换位置i
* @param j 交换位置j
*/
private static void swap(int[] array, int i, int j) {
if (i != j) {
array[i] = array[i] ^ array[j];
// 相当于array[i] ^ array[j] ^ array[j]
array[j] = array[i] ^ array[j];
// 相当于array[i] ^ array[j] ^ array[i]
array[i] = array[i] ^ array[j];
}
}
/**
* 打印数组元素
*
* @param array 数组
* @param sortType 排序类型
*/
private static void display(int[] array, String sortType) {
Arrays.stream(array).forEach(x -> System.out.print(x + " "));
System.out.println(sortType);
}
/**
* 通过反射调用指定排序方法
*
* @param sortType 排序方法
*/
public static void sort(String sortType) {
try {
int[] array = new int[]{11, 56, 35, 62, 97, 21, 36, 33, 86, 81, 35, 8, 135, 235, 4567};
Class<?> clz = Class.forName(NumberSort.class.getName());
Method m = clz.getDeclaredMethod(sortType, int[].class);
m.invoke(null, new Object[]{array});
display(array, sortType);
} catch (Exception e) {
e.printStackTrace();
}
}
public static void main(String[] args) {
sort("bubbleSort");
sort("quickSort");
sort("threeWayQuickSort");
sort("selectionSort");
sort("heapSort");
sort("straightInsertSort");
sort("shellSort");
sort("mergeSort");
sort("bucketSort");
sort("countingSort");
sort("radixSort");
}
}
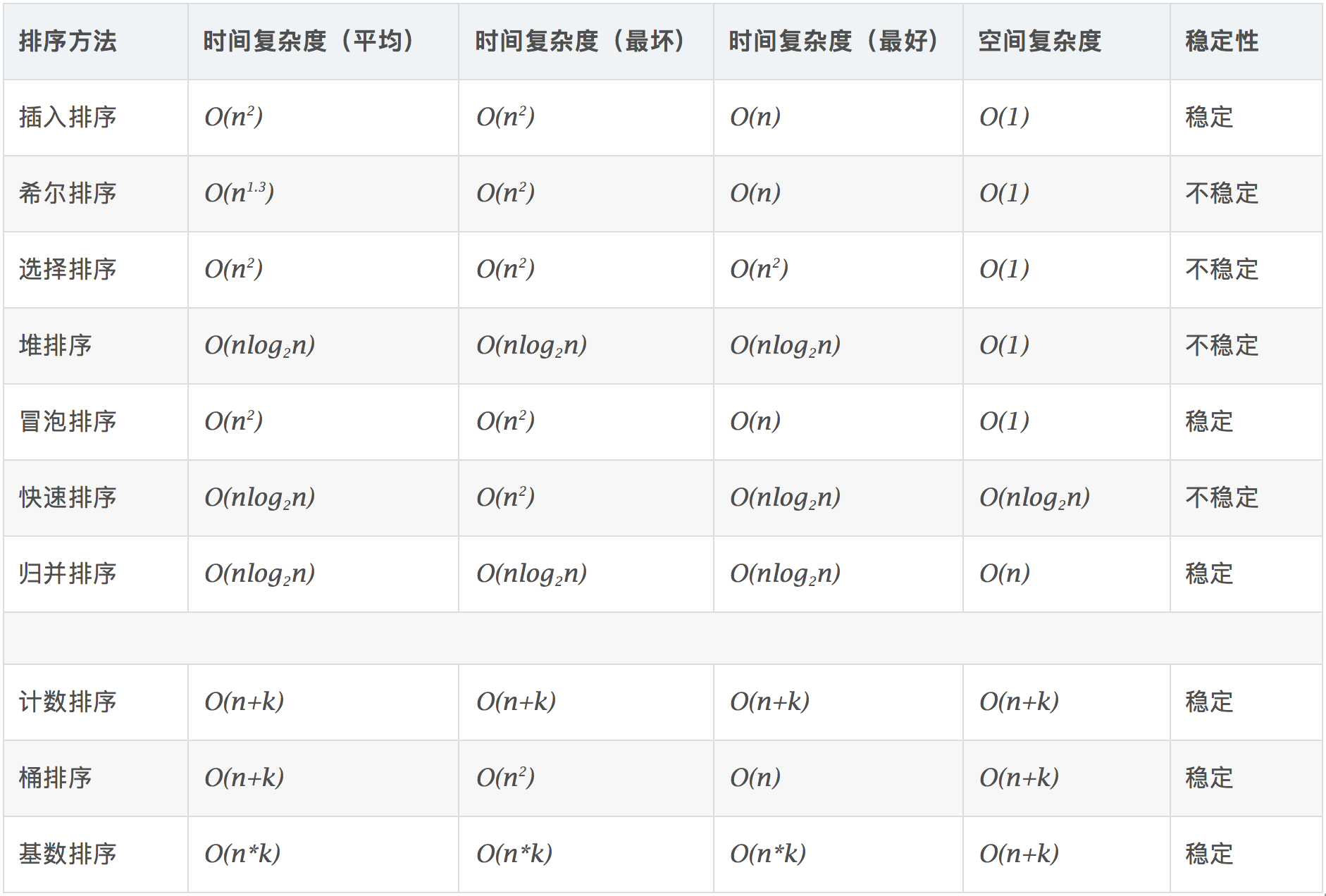
影响排序的因素有很多,平均时间复杂度低的算法并不一定就是最优的。相反,有时平均时间复杂度高的算法可能更适合某些特殊情况。同时,选择算法时还得考虑它的可读性,以利于软件的维护。一般而言,需要考虑的因素有以下四点:
根据待排序元素的个数n,分析如下:
原文:https://www.cnblogs.com/sheung/p/14591411.html