动态规划 最长单调递增子序列

1.问题

设计一个O(N^2)时间的算法，找出由n个数组成的序列的最长单调递增子序列

2.题目分析

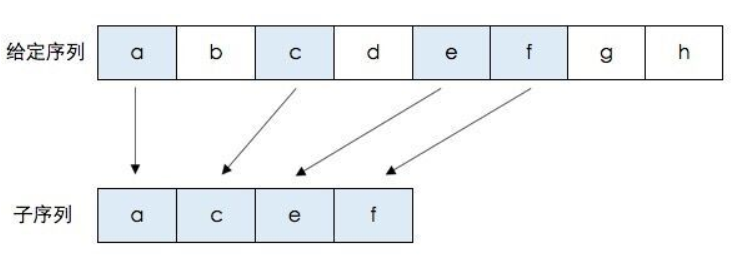
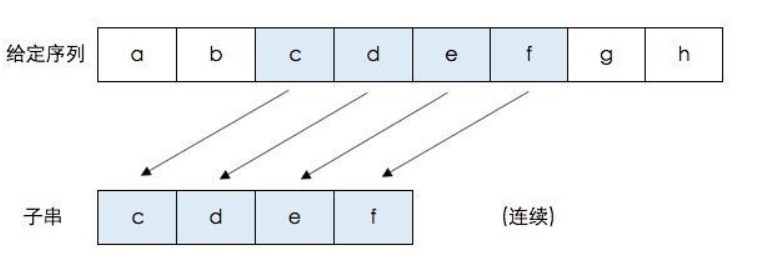
最长公共子序列（longest common sequence）和最长公共子串（longest common substring）的区别

• 子序列：即一个给定的序列的子序列，就是将给定序列中零个或多个元素去掉之后得到的结果。

• 子串：给定串中任意个连续的字符组成的子序列称为该串的子串。

3.解题思路

数组a[]为输入的原始序列，用一个数组b[]表示a[]升序排序后的序列，找a[]中最长的单调递增数列，可以将这个问题转化为，寻找a、b两个数组最长的公共子序列。

• 最优子结构：a 序列的前 i 个元素和b序列的前ｊ个元素的最长公共子序列一定是ａ，ｂ的最长公共子序列的一部分。

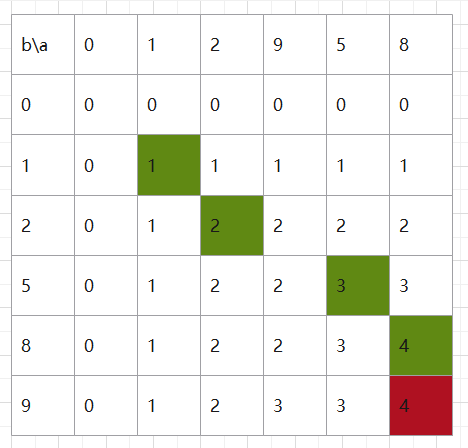
• 状态转移方程：

  对于 a 的前 i 个元素和 b 的前 j 个元素, t [i] [j]是公共子序列的最大长度。设公共子序列中的最后一个元素是zx

  ①a[i-1] = b[j-1] : t [i] [j] = t [i-1] [j-1] +1 
  

  最后一个元素相同，zx必定是两序列的最后一个元素。

  ②a[i-1] != b[j-1]: t [i] [j] = max(t[i-1][j], t[i][j-1])
  

  最后一个元素不同，那么zx是 a 的前 i-1 个元素和 b 的前 j 个元素最长公共子序列的最后一个元素，或者 a 的前 i 个元素和 b 　的前 j-1 个元素最长公共子序列的最后一个元素，因为原问题需要的是最优的解，因此选长度较大的。
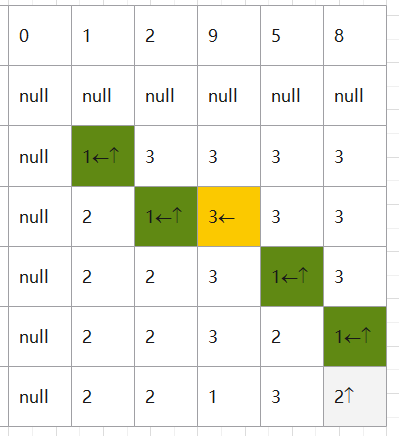
  （你可以通过下面这两幅图，理解代码中，dp和m在干什么）
  
  

代码实现

import java.io.*;
import java.util.Arrays;
public class Main {
	public static void main(String[] args) throws IOException {
		StreamTokenizer st=new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
		st.nextToken();
		int n=(int)st.nval;	//输入序列长度
		int[] a=new int[n];
		for(int i=0;i<n;i++) {	//输入序列
			st.nextToken();
			a[i]=(int)st.nval;
		}
		maxlist(a,n);
	}	
    public static int maxlist(int a[],int n) {
        int b[]=new int[n];
        for(int i=0;i<n;i++) {
            b[i]=a[i];
        }
        Arrays.sort(b);	//排序
        int dp[][]=new int [n+1][n+1];	//设置为n+1*n+1，为了防止元素溢出
        int m[][]=new int [n+1][n+1];	//dp用来寻找问题的最优解，m用来记录dp是通过哪一个子问题得到的
        for(int i=0;i<n;i++) {	//初始化dp
            dp[i][0]=dp[0][i]=0;	//边界设为0
        }
        for(int i=1;i<=n;i++){	
            for(int j=1;j<=n;j++){
                if(a[i-1]==b[j-1]){	//a[i]和b[i]从下标0开始比较是否相等
                    dp[i][j]=dp[i-1][j-1]+1;
                    m[i][j]=1;
                }
                else{
                    dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
                    m[i][j]=dp[i-1][j]>dp[i][j-1]?2:3;
                }
            }
        }
        int i=n,j=n;
        int[] sub=new int [n];
        int k=0,limit=Integer.MAX_VALUE;
        while(i>=0&&j>=0){
            if(m[i][j]==1&&a[i-1]<limit){
                limit=a[i-1];
                sub[k++]=a[i-1];
                i--;j--;
            }
            else if(m[i][j]==2)
                i-=1;
            else 
                j-=1;
        }
        for(i=k-1;i>=0;i--)
            System.out.print(sub[i]+" ");
        return dp[n][n];
    }
}

4.时间复杂度：Ｏ（ｎ＾２）

动态规划 最长单调递增子序列

原文：https://www.cnblogs.com/runaway-code/p/14601747.html