在高中数学中,经常会碰到求线段长度或者直线与曲线相交得到的弦的长度,所用到的求解公式与所处的坐标系和采用的方法都有关。
【公式】:\(|AB|=\sqrt{1+k^2}\cdot |x_1-x_2|\), 推导过程[1]
【使用条件】:在直角坐标系下使用,针对直线的普通方程和曲线的普通方程,说明:\(k\) 为直线的斜率,直线和曲线的交点为 \(A(x_1,y_1)\) , \(B(x_2,y_2)\) ;
设直线和圆的交点为\(A(x_1,y_1),B(x_2,y_2)\),
联立得到方程组,\(\left\{\begin{array}{l}{2x-y-3=0}\\{x^2+y^2-4y-12=0}\end{array}\right.\)
消去\(y\)得到,\(x^2+(2x-3)^2-4(2x-3)-12=0\),整理得到,\(5x^2-20x+9=0\),
由韦达定理得到,\(x_1+x_2=4\),\(x_1x_2=\cfrac{9}{5}\),
由弦长公式得到,\(|AB|=\sqrt{1+k^2}|x_1-x_2|\)\(=\sqrt{1+2^2}\sqrt{(x_1+x_2)^2-4x_1x_2}\)
\(=\sqrt{5}\sqrt{16-\cfrac{36}{5}}=2\sqrt{11}\)。
【公式】:\(|AB|=|t_1-t_2|\),可以类比一维数轴上的两点间的距离公式来理解;
【使用条件】: 在直角坐标系下,针对直线的参数方程和曲线的普通方程使用,还要注意直线的参数方程在使用时必须验证其是否为标准形式。说明:其中点 \(A\),\(B\) 为直线和曲线的交点,直线上的点 \(A\),\(B\) 所对应的参数分别为 \(t_1\)和 \(t_2\) .
解析:将直线的参数方程 \(\left\{\begin{array}{l}x=-\cfrac{\sqrt{3}}{2} t\\y=2+\cfrac{t}{2}\end{array}\right.\) (\(t\) 为参数)代人曲线方程 \(y^{2}-3 x^{2}=0\),
得 \(t^{2}-t-2=0\),解得 \(t_{1}=2\), \(t_{2}=-1\),
由参数的儿何意义知,截得的线段长为 \(|t_1-t_2|=|2-(-1)|=3\).
解析:直线的参数方程 \(\left\{\begin{array}{l}x=1+2t\\y=3t\end{array}\right.\) 可以化成 \(\left\{\begin{array}{l}x=1+\cfrac{2}{\sqrt{13}}(\sqrt{13}t)\\y=\cfrac{3}{\sqrt{13}}(\sqrt{13} t)\end{array}\right.,\)
将直线方程 \(\left\{\begin{array}{l}x=1+2t\\y=3 t\end{array}\right.,\) 代人 \(y^{2}=3x\),
得 \(3t^{2}-2t-1=0\), 解得 \(t_{1}=-\cfrac{1}{3}, t_{2}=1\),
由参数的儿何意义知,所得的弦长为 \(\sqrt{13}|t_{2}-t_{1}|=\cfrac{4\sqrt{13}}{3}\).
【公式】\(AB=\sqrt{\rho_{_{A}}^2+\rho_{_{B}}^2-2\cdot \rho_{_{A}}\cdot\rho_{_{B}}\cos(\theta_1-\theta_2)} ①\) 或 \(|AB|=|\rho_{_{A}}-\rho_{_{B}}| ②\)
【使用条件】 在极坐标系下使用,且直线和曲线的方程形式都是极坐标方程;其中点 \(A(\rho_{_{A}},\theta_1)\) , \(B(\rho_{_{B}},\theta_2)\) ,公式 ① 其实就是由三角形余弦定理得到的,公式 ② 是公式 ① 的特例,当点 \(O\),\(A\),\(B\)三点共线时,\(\theta_1=\theta_2\),此时可以将公式 ① 简化为公式 ② ;本来公式 ② 不应该单列出来,但是实际考察中,使用更多的是公式 ② ,故单列便于记忆和比较。
(1). 以坐标原点为极点,\(x\) 轴的正半轴为极轴建立极坐标系,求 \(C\) 的极坐标方程。
分析:由于极坐标方程中只有 \(\rho\) 和 \(\theta\),
故只要将\(x=\rho\cdot cos\theta\)和\(y=\rho\cdot sin\theta\)代入圆\(C\)的直角坐标方程为\((x+6)^2+y^2=25\),
整理可得\(\rho^2+12\rho cos\theta+11=0\)。
(2). 直线 \(l\) 的参数方程为 \(\begin{cases} x=t\cdot cos\alpha \\ y=t\cdot sin\alpha \end{cases}(t为参数)\), \(l\) 与 \(C\) 交于 \(A\) 、 \(B\) 两点,\(|AB|=\sqrt{10}\),求直线 \(l\) 的斜率。
【法1】:极坐标法,由于此次为重点介绍极坐标的用法,故将此方法排在前面。
圆\(C\)的极坐标方程是\(\rho^2+12\rho cos\theta+11=0\)。
将直线的参数方程两式相除得到,\(y=tan\alpha x\),即\(y=kx\),
则直线的极坐标方程为\(\theta=\alpha(\rho\in R)\)
将直线的极坐标方程代入圆\(C\)的极坐标方程是\(\rho^2+12\rho cos\theta+11=0\),
得到圆\(C\)的极坐标方程是\(\rho^2+12\rho cos\alpha+11=0\),
设点\(A\)的极坐标方程为\((\rho_1,\alpha)\),点\(B\)的极坐标方程为\((\rho_2,\alpha)\),
则\(\rho_1+\rho_2=-12cos\alpha\),\(\rho_1\cdot \rho_2=11\),
由\(|AB|=|\rho_1-\rho_2|= \sqrt{(\rho_1+\rho_2)^2-4\rho_1\rho_2}=\sqrt{10}\),
解得\(cos^2\alpha=\cfrac{54}{144}=\cfrac{3}{8}\),
又由图可知\(\alpha\in [0,\pi)\),故\(cos\alpha=\pm\cfrac{\sqrt{6}}{4}\),
则有\(sin\alpha=\cfrac{\sqrt{10}}{4}\)
故\(tan\alpha=\cfrac{sin\alpha}{cos\alpha}=\cfrac{\cfrac{\sqrt{10}}{4} }{\pm\cfrac{\sqrt{6}}{4}} =\pm\cfrac{\sqrt{15}}{3}\)。
故直线\(l\)的斜率为\(\pm\cfrac{\sqrt{15}}{3}\)。
【法2】参数方程法,
分析:本题目的求解要用到直线的参数方程的几何意义。
将直线\(l\)的参数方程代入圆\(C\)的直角坐标方程,化简整理为\(t^2+12t cos\alpha+11=0\),
可设点\(A、B\)分别对应参数\(t_1,t_2\),则\(\begin{cases} t_1+ t_2=-12cos\alpha\\t_1\times t_2=11\end{cases}\),
\(|AB|=|t_1-t_2|= \sqrt{(t_1+t_2)^2-4t_1t_2}=\sqrt{10}\),
解得\(cos^2\alpha=\cfrac{54}{144}=\cfrac{3}{8}\),
又由图可知\(\alpha\in [0,\pi)\),故\(cos\alpha=\pm\cfrac{\sqrt{6}}{4}\),则有\(sin\alpha=\cfrac{\sqrt{10}}{4}\)
故\(tan\alpha=\cfrac{sin\alpha}{cos\alpha}=\cfrac{\frac{\sqrt{10}}{4} }{\pm\frac{\sqrt{6}}{4}} =\pm\cfrac{\sqrt{15}}{3}\)。
故直线\(l\)的斜率为\(\pm\cfrac{\sqrt{15}}{3}\)。
【法3】平面几何法,如图所示,这样的直线应该有两条,且其斜率互为相反数,现重点求解图中的直线\(AB\)的斜率,
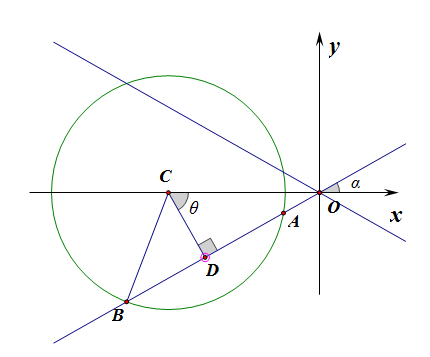
在\(Rt\Delta BCD\)中,半径为\(BC=5\),半弦长为\(BD=\cfrac{\sqrt{10}}{2}\),
利用勾股定理求得,弦心距\(CD=\cfrac{3\sqrt{10}}{2}\)
在\(Rt\Delta OCD\)中,\(OC=6\),\(CD=\cfrac{3\sqrt{10}}{2}\)
求得\(cos\angle OCD=cos\theta=\cfrac{\sqrt{10}}{4}\)
从而\(sin\alpha=\cfrac{\sqrt{10}}{4}\),\(cos\alpha=\cfrac{\sqrt{6}}{4}\),
即\(k=tan\alpha=\cfrac{\sqrt{10}}{\sqrt{6}}=\cfrac{\sqrt{15}}{3}\),
故满足条件的直线\(AB\)有两条,其斜率为\(\pm\cfrac{\sqrt{15}}{3}\)。
设直线方程为\(y=kx+b\),两个交点为点\(A(x_1,y_1)\),\(B(x_2,y_2)\);
则由平面内任意两点间的距离公式可得,
\(|AB|=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}=\sqrt{(x_1-x_2)^2+[(kx_1+b)-(kx_2+b)]^2}\)
\(=\sqrt{(x_1-x_2)^2+k^2(x_1-x_2)^2}=\sqrt{1+k^2}\cdot \sqrt{(x_1-x_2)^2}\)
\(=\sqrt{1+k^2}\cdot |x_1-x_2|\)
即弦长公式:\(|AB|=\sqrt{1+k^2}\cdot |x_1-x_2|\)
\(|AB|=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}=\sqrt{(\frac{y_1-b}{k}-\frac{y_2-b}{k})^2+(y_1-y_2)^2}\)
\(=\sqrt{\frac{(y_1-y_2)^2}{k^2}+(y_1-y_2)^2}=\sqrt{1+\frac{1}{k^2}}\cdot \sqrt{(y_1-y_2)^2}\)
\(=\sqrt{1+\frac{1}{k^2}}\cdot |y_1-y_2|\)
即弦长公式:\(|AB|=\sqrt{1+\frac{1}{k^2}}\cdot |y_1-y_2|\)
故弦长公式:\(|AB|=\sqrt{1+k^2}\cdot |x_1-x_2|=\sqrt{1+\frac{1}{k^2}}\cdot |y_1-y_2|\)
具体使用时,如下所示,为了和韦达定理相联系。
\(|AB|=\sqrt{1+k^2}\cdot |x_1-x_2|=\sqrt{1+k^2}\cdot\sqrt{ |x_1-x_2|^2}\)\(=\sqrt{1+k^2}\cdot\sqrt{ x_1^2+x_2^2-2x_1x_2}\)\(=\sqrt{1+k^2}\cdot\sqrt{ x_1^2+x_2^2+2x_1x_2-
4x_1x_2}\)\(=\sqrt{1+k^2}\cdot\sqrt{(x_1+x_2)^2-4x_1x_2}\)
\(|AB|=\sqrt{1+(\cfrac{1}{k})^2}\cdot\sqrt{(y_1+y_2)^2-4y_1y_2}\) ??
原文:https://www.cnblogs.com/wanghai0666/p/14604695.html