【Graphics Tricks】01_描边

————————————————————————————

阅读说明：作者还在入门中，文章如有错误，请务必指正，万分感谢！

————————————————————————————

1 边缘检测

　　边缘检测是屏幕后处理中图像描边方法（如后文的2.1和2.2）的技术核心，因此这里先对边缘检测的相关知识点进行简要梳理。

1.1 卷积

　　计算机世界是离散的，所以这里暂不考虑卷积的连续情况。

1.1.1 一维离散卷积

　　对一维离散序列X = (x₁, x₂, x₃, x₄, x₅)使用卷积核C = (c₁, c₂, c₃)进行卷积操作，得到的结果仍然是一个长度为5的一维序列R = (r₁, r₂, r₃, r₄, r₅)。R中每个元素r_i (i=1,2…5)的生成过程如下：①将卷积核C的中心c₂对准x_i，②从X中截取C的长度能覆盖到的元素(x_i-1, x_i, x_i+1)，③将截取的X的元素和C的元素反向相乘，得到新序列 (x_i-1*c₃, x_i*c₂, x_i+1*c₁)，④将新序列的每个元素累加，得到的结果就是r_i。比如，r₃ = c₃*x₂ + c₂*x₃ + c₁*x₄。至于X的边界元素则可以用填充数值的方式来使卷积操作变得可行，比如可以向X的边界填充0，使之成为序列 (0, x₁, x₂, x₃, x₄, x₅, 0)，这样位于边界的x₁对应的卷积结果为r₁ = c₃*0 + c₂*x₁ + c₁*x₂，位于边界的x₅同理。

1.1.2 二维离散卷积

       二维离散数组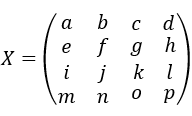可以看作一维离散序列 (a, b, c, d, e, f…n, o, p) 在二维空间上的重新排布，二维卷积核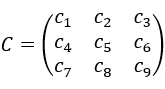也可以看作一维卷积核 (c₁, c₂, c₃, c₄…c₉)在二维空间上的重新排布，那么二维的卷积操作就很好理解了：在将C的中心元素c₅对齐X的元素比如f后，截取X能被C覆盖的元素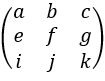，将它们展开成一维的 (a, b, c, e, f, g, i, j, k) 和 (c₁, c₂, c₃, c₄, c₅, c₆, c₇, c₈, c₉) 后，反向相乘再累加即可得到结果a*c₉ + b*c₈ + c*c₇ + e*c₆ + f*c₅ + g*c₄ + i*c₃ + j*c₂ + k*c_1.

1.1.3 图像处理中的卷积

① 卷积的本质其实是对图像中的每个像素做遍历，将每个像素的值调整成周围一圈像素值的加权累加和，也就是让每个像素在保留原本信息的同时携带上周围一圈像素的信息，而卷积核中的每个元素就是对应像素的贡献权重。因此不同的卷积核能实现对图像的不同处理，除了本文要介绍的边缘检测外，另一个重要的卷积应用是模糊。

② 卷积的初始定义是将卷积核元素与被处理元素“反向”相乘，但为了方便起见，我们可以在实际应用中采用“正向”相乘的方式，只要对卷积核元素位置做相应变换，这和初始的卷积定义得到的结果是一样的。

③ 在图像处理中，卷积边界的处理方式取决于纹理的wrap mode，比如wrap mode为clamp，就说明超出边界的元素值就等于边界值。

1.2 边缘检测算子

1.2.1 Roberts算子

　　Gx检测右下-左上对角线上的边缘，Gy检测左下-右上对角线上的边缘。所谓边缘就是指图像的像素值产生“突变”的地方，因此abs(Gx)和abs(Gy)的值如果较大，就说明该方向上有边缘。

1.2.2 Prewitt算子

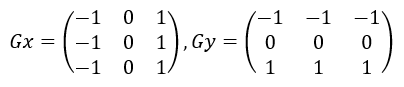
       Gx检测横向的边缘，Gy检测纵向的边缘。

1.2.3 Sobel算子

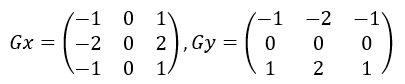
　　和Prewitt算子一样，Gx检测横向的边缘，Gy检测纵向的边缘。不同之处在于，Sobel算子加强了中心像素的邻近像素的权重。

2 描边方法

2.1 基于色彩纹理的描边

① 一种屏幕后处理方法，将渲染好的场景作为一张纹理输入shader，使用卷积操作来检测图像（通常是明度值）的边缘信息。

② 描边结果容易夹带光影信息和纹理信息（见图1）。

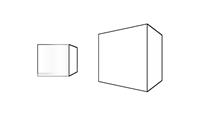
Fig.1. 原始图像（左）和描边结果（右）

2.2 基于深度法线纹理的描边

① 一种屏幕后处理方法，是对2.1方法的改进。

② 深度纹理和法线纹理可以一起使用（只要在一种纹理上检测出边缘，即认为边缘存在），从而增加边缘检测效果的健壮性。如果只用深度纹理或法线纹理，某些边缘会检测不出来。

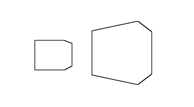
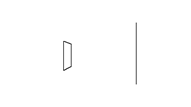
Fig. 2. 仅使用深度纹理（左）和仅使用法线纹理（右）的边缘检测效果

③ 多个方向的检测也可以一起使用，以增加边缘检测效果的健壮性。

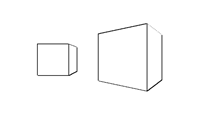
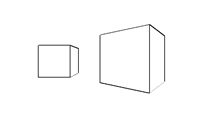
Fig. 3. 仅使用左上-右下方向（左）和仅使用右上-左下方向（右）的边缘检测效果

④ 检测边缘是否存在时（梯度差的绝对值是否大于阈值），可以使用随深度值增大而减小的阈值，从而造成近粗远细的描边效果。

2.3 基于观察角度和表面法线的描边

① 使用表面法线和观察角度的点乘来获取描边信息。

② 限制比较大，比较适合面与面间过度较圆润的物体（如图4）。

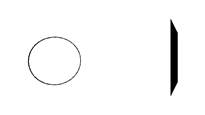
Fig.4. 原始模型（左）和描边效果（右）

2.4 基于轮廓边检测的描边

① 判断从视角到边缘的方向v与边缘相邻两个三角形的法线n是否同向。

② 需要借助几何着色器，开销昂贵，且一些引擎如Unity的几何着色器并不支持triangleadj，无法提供邻接三角形的信息。

2.5 过程式几何轮廓渲染

① 使用两个pass。第一个pass先渲染模型背面，并将顶点沿法线方向拓展，形成轮廓线；第二个pass再渲染模型正面。

② 此方法不适用于正方体这类的平整模型，会在面与面的交接处出现断层（如图5）。

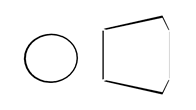
Fig.5. 原始模型（左）和描边效果（右）

③ 对于复杂模型（可能有内凹的地方），最好在向外拓展顶点时将法线的z值统一方向（统一远离镜头），这样可以避免拓展后的模型背面遮挡住模型正面的情况，如图6.

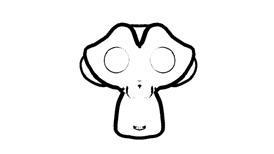
Fig.6. 未统一法线z轴的描边（左）和统一法线z轴的描边（右）

【Graphics Tricks】01_描边

原文：https://www.cnblogs.com/rbcl-ljh/p/14608945.html