有N个物品和一个容量是v的背包,每个物品有两个属性:体积\(v_i\)和价值\(w_i\)。
我们要在背包装得下的情况下让选出的物品总价值最大。
进阶可以看看背包九讲。
动态规划是没有模板的,他的代码就是一些循环,他的核心在于状态的表示和状态的转移,比较偏向于数学的思考。

每件物品只能用一次。
https://www.acwing.com/problem/content/2/
动态规划问题一般从两方面考虑:状态表示和状态计算。状态就是一个未知数,背包问题一般是一个两维的。状态表示就是思考以下我们整个状态用几维来表示。状态计算就是我们如何能把我们的状态一步一步地算出来。
DP的优化就是对DP的代码/方程进行一个等价变形。比如背包最好是用一维来写,但是我们考虑时要从最朴素开始考虑。
从集合的角度来理解DP,每一个状态都是表示一个集合,我们需要考虑清楚的就是f[i,j]表示的是哪一个集合。比如背包问题就是所有选法的一个集合。状态计算就是集合的划分。状态计算考虑的就是如何把我们当前的集合划分成若干个更小的子集,使得每一个子集我们都可以算出来。
在本题里,集合就是一个选法的集合,记录的是我们是选择1,2,3还是1,3,5件物品。
把所有的f[i,j]全部算出来之后,答案应该是f[N,V]。
划分的原则就是:
具体划分图如下:
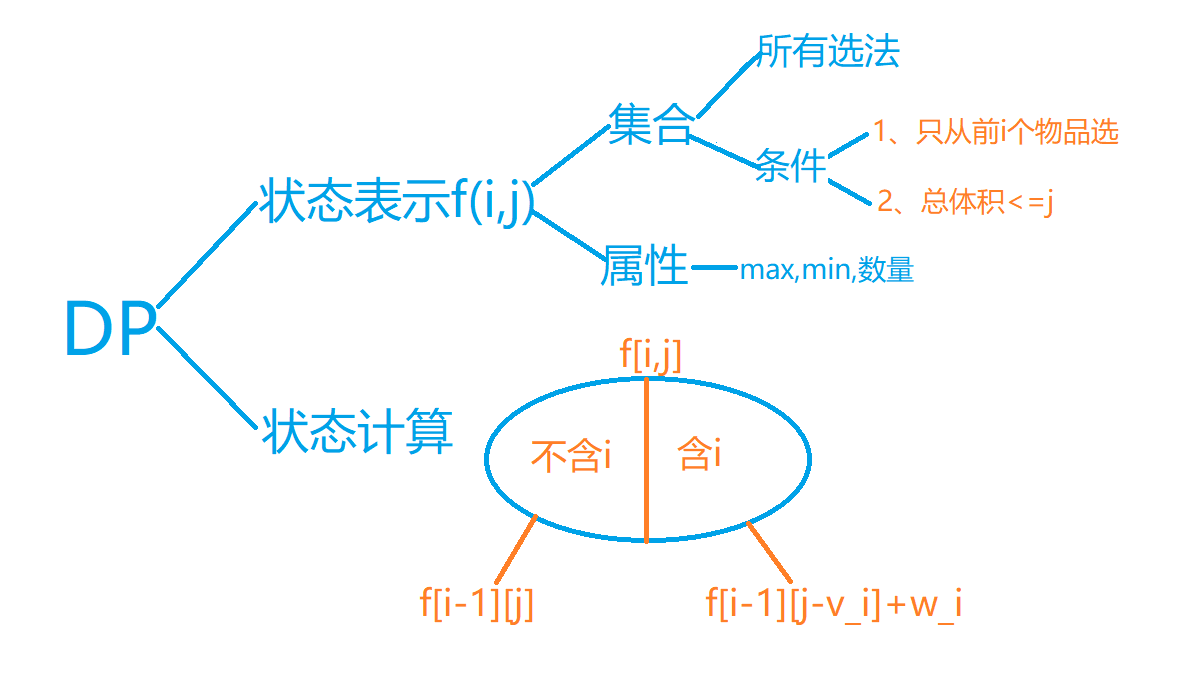
不含i:就是1i中选,总体积不超过j,且不包含第i个元素。实际就是1(i-1)去选。也就是\(f[i-1,j]\)。
含i:因为都包含i,那么就可以考虑成从1~i-1选,且总体积\(\le j-i\)的集合。即\(f[i-1,j-v_i]+w_i\)。
那么最后的结果就是\(Max(f[i-1,j],f[i-1,j-v_i]+w_i)\)就可以了。
#include<iostream>
using namespace std;
const int N = 1010;
int n,m;
int v[N],w[N]; // 表示容量和价值
int f[N][N]; // 表示所有的状态
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
// 要枚举所有状态即f[0~n][0~m],f[0][0~m]表示选择0件物品总体积不超过都为0,1,2...m,结果都为0
// n是物品数量,m是背包容量
for(int i = 1; i <= n; i++)
for(int j = 0; j <= m; j++)
{
f[i][j] = f[i-1][j];
//只有v[i] <= j才可以选择第i件物品
if(j >= v[i]) f[i][j] = max(f[i][j], f[i-1][j-v[i]] + w[i]);
}
cout << f[n][m] << endl;
return 0;
}
可以发现f[i]在计算时实际上只用到f[i-1]这层,f[i-1]~f[0]这些层是没被使用的,我们的j不管是j还是j-v_i都是<=j的而不是在j的两侧,所以我们可以改成一维数组来算。
#include<iostream>
using namespace std;
const int N = 1010;
int n,m;
int v[N],w[N]; // 表示容量和价值
int f[N]; // 表示所有的状态
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
// 要枚举所有状态即f[0~n][0~m],f[0][0~m]表示选择0件物品总体积不超过都为0,1,2...m,结果都为0
// n是物品数量,m是背包容量
for(int i = 1; i <= n; i++)
// for(int j = m; j >= v[i]; j--)
for(int j = 0; j <= m; j++)
{
// f[j] = f[j];这样就是一个恒等式了可以直接删除
// 如此这个循环j<v[i]时直接就会跳过去
// 所以0~v[i-1]是没有意义的,j就可以从v[i]开始循环
// 判断也可以删除了
// if(j >= v[i]) f[i][j] = max(f[i][j], f[i-1][j-v[i]] + w[i]);
f[j] = max(f[j], f[j-v[i]] + w[i]);
// 现在和原先二维并不等价,它实际等价于
// f[i][j] = max(f[i][j], f[i][j-v[i]] + w[i])
// 因为j-v[i]是一定<j的,j是从小到大枚举的,在算f[j]时
// f[j-v[i]]在第i层已经被计算过了,所以他实际是第i层的
// j-v[i]
// 想解决这个问题只需要将循环顺序变成从大到小就可以了
// 如现在所示f
// 这样在计算时由于f[j-v[i]]还没有被更新过,存储的就是
// 第i-1层的f[j-v[i]],就等价于
// f[i][j] = max(f[i][j], f[i-1][j-v[i]] + w[i])
// 实际就是从大到小枚举的话,j-v[i]<j
// j才刚更新,比j小的j-v[i]自然没更新
}
cout << f[m] << endl;
return 0;
}
每件物品有无限个
可以按照第i件物品选n个来划分集合。
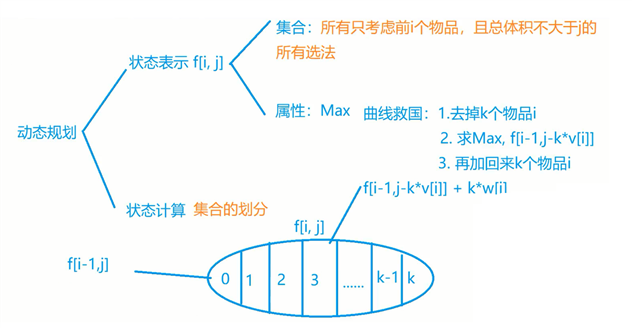
所以最后的状态转移方程:\(f[i,j] = f[i-1,j-v[i]*k] + w[i]*k\)。其中k为第i个物品的数量。
这时需要有3重循环是比较慢的,我们可以把它优化成2维的。
题目链接:https://www.acwing.com/problem/content/3/
朴素做法代码如下:
// 最坏情况下是O(n*n2)的
// 完全背包问题是可以优化成两维的
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int f[N][N];
int n,m;
int v[N],w[N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
// 实现状态转移方程,枚举所有状态
for(int i = 1; i <= n; i++)
for(int j = 0; j <= m; j++)
for(int k = 0; k*v[i] <= j; k++) // 枚举物品的数量
f[i][j] = max(f[i][j], f[i-1][j-k*v[i]] + k*w[i]);
cout << f[n][m];
return 0;
}
优化:
把这个状态转移方程展开:
f[i,j] = Max(f[i-1,j],f[i-1,j-v]+w),f[i-1,j-2v]+2w,f[i-1,j-3v]+3w,...)?它实际就是取最大值。
那么我们对比一下:
f[i,j-v] = Max( f[i-1,j-v], f[i-1,j-2v]+w, f[i-1,j-3v]+2w,...)?
经过对比我们可以发现:
f[i,j]和f[i,j-v]很相似,前者的每一项都比他对应的后者多了一项w,所以:

即:f[i,j] = Max(f[i-1,j],f[i,j-v]+w)。
原先需要枚举k个状态,现在只需要枚举两个状态,减少一重循环,时间复杂度为O(\(n^2\))。
完全背包也可以优化成一维:
做等价变形就可以
二维代码如下图所示
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int f[N][N];
int n,m;
int v[N],w[N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
// 实现状态转移方程,枚举所有状态
for(int i = 1; i <= n; i++)
for(int j = 0; j <= m; j++)
{
f[i][j] = f[i-1][j];
if(j >= v[i]) f[i][j] = max(f[i][j], f[i][j-v[i]]+w[i]);
}
cout << f[n][m];
return 0;
}
做等价变形删掉一个维度就可以
把前面的删除,f[N] [N]变成f[N],f[i] [j] = f[i-1] [j]变成f[j] = f[j]
当j<v[i]时,这个循环会直接pass,所以我们从v[i]开始第二个循环,if判断就可以删除了
f[i] [j] = max(f[i] [j], f[i] [j-v[i]]+w[i])就变成f[j] = max(f[j], f[j-v[i]]+w[i])
一维代码如下:
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int f[N];
int n,m;
int v[N],w[N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
// 实现状态转移方程,枚举所有状态
for(int i = 1; i <= n; i++)
for(int j = v[i]; j <= m; j++)
f[j] = max(f[j], f[j-v[i]]+w[i]);
// 这里不需要将j从大到小进行
// 由于j是从小到大枚举的且j-v[i]<j
// 所以在算f[j]时f[j-v[i]]已经被算过了
// 这里的j-v[i]实际是f[i][j-v[i]]和状态转移方程一致
cout << f[m];
return 0;
}
思考:
为什么0,1背包和完全背包的一维代码最后只差看一个循环顺序呢,一个从小到大,一个从大到小。
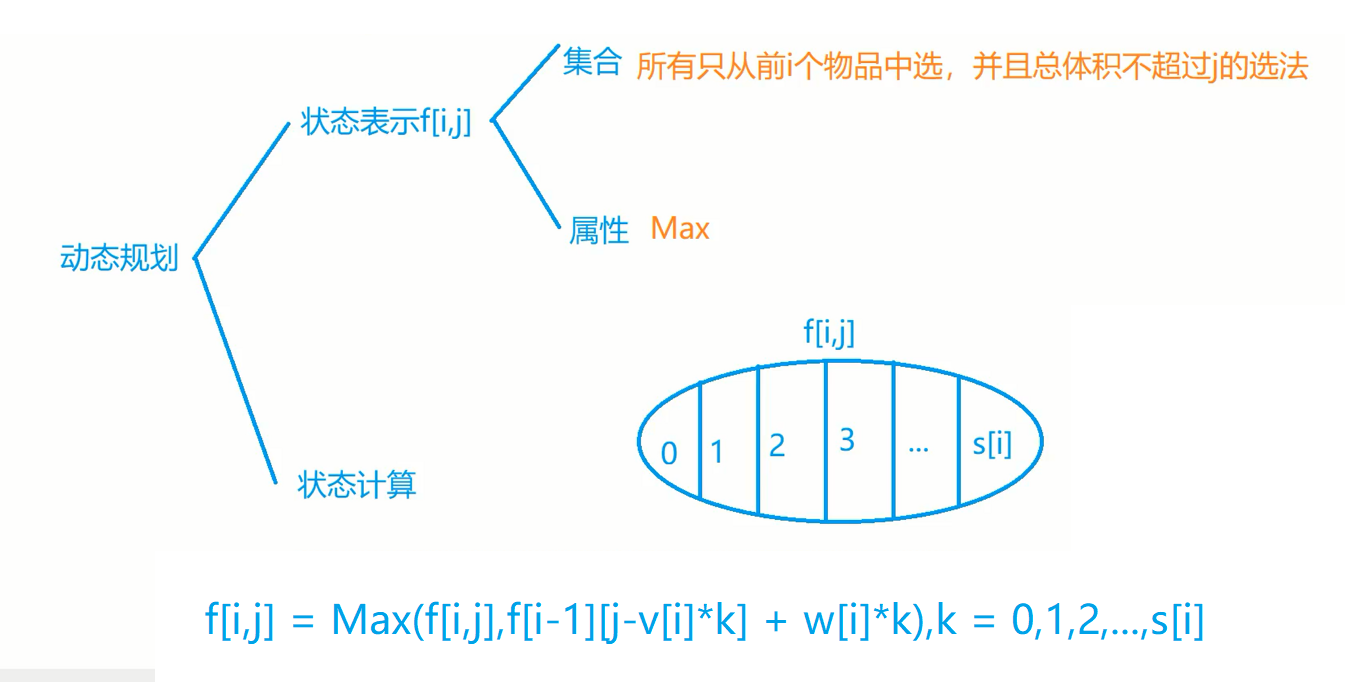
每个物品最多有\(S_i\)个。
题目链接:https://www.acwing.com/problem/content/5/
暴力做法直接:
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 110;
int f[N][N];
int n,m;
int v[N],w[N],s[N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> v[i] >> w[i] >> s[i];
// 实现状态转移方程,枚举所有状态
for(int i = 1; i <= n; i++)
for(int j = 0; j <= m; j++)
for(int k = 0; k <= s[i] && k*v[i] <= j; k++) // 枚举物品的数量
f[i][j] = max(f[i][j], f[i-1][j-k*v[i]] + k*w[i]);
cout << f[n][m];
return 0;
}
优化:
使用了一种二进制的优化方式。
比如我们某一件物品有1023个,我们真的需要从0一直枚举到1023吗?
我们可以把若干个第i件物品打包在一起来考虑,比如我们打包成10组
第一组1个吗,第二组2个,第3组四个...即1,2,4,8,... ,512个
每组最多只能选一次,我们一定能用这10组拼凑出1023中的任意一个数字。
每一个打包起来的第i个物品我们就可以把他看作0,1背包中的一个物品只能选择一次,即我们就是用了10个新的物品表达原来的第i个物品。这样原来需要枚举1023次,现在就只需要10次,这是log的关系。
假设s = 200
那么就是1,2,4,8,16,32,64,128,73
128不能选择,因为选择之后就是0~255。1+2+...+64 = 127,200-127=73。
如此,假设第i个物品有Si个,我们就可以把它拆成\(log^{S_i}\)个。再对所有新的物品做一个0,1背包问题就可以了。
原先是O(N * V * S),现在是O(N * \(log^s\) *V)。
优化后代码如下:
// C++ 1s内最多算1亿次,如果暴力解决的话
// 1000*2000*2000 = 4亿次一定超时
// f[i,j] = max(f[i-1,j],f[i-1,j-v]+w,f[i-1,j-2v]+2w,...,f[i-1,j-sv]+sw)
// f[i,j-v] = max( f[i-1,j-v, f[i-1,j-2v]+w ,...,f[i-1,j-sv]+(s-1)w,f[i-1,j-(s+1)v]+sw)
// 给定1,2,4,6,7,8,9,能求出除了最后一个数以外即不包括9的最大值吗,max不可以做到,因为max无法做减法
// 所以无法直接用完全背包优化方式优化多重背包问题
// s个可以分解成log^s组,对所有新的物品做一个o,1背包
// 时间复杂度为可以由O(Nvs)优化为O(N*logs*v)
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 25000; // 1000*2000*12 = 24000,所以开了25000
const int M = 2010;
int f[N];
int n,m;
int v[N],w[N];
int main()
{
cin >> n >> m;
int cnt = 0;
for(int i = 1; i <= n; i++)
{
int a,b,s;
cin >> a >> b >> s; // 体积,价值,个数
int k = 1;
while(k <= s)
{
cnt++;
v[cnt] = a*k;
w[cnt] = b*k;
s -=k;
k *= 2;
}
if(s > 0)
{
cnt++;
v[cnt] = a*s;
w[cnt] = b*s;
}
}
n = cnt;
for(int i = 1; i <= n; i++)
for(int j = m; j >= v[i]; j--)
f[j] = max(f[j],f[j-v[i]]+w[i]);
cout << f[m] << endl;
return 0;
}
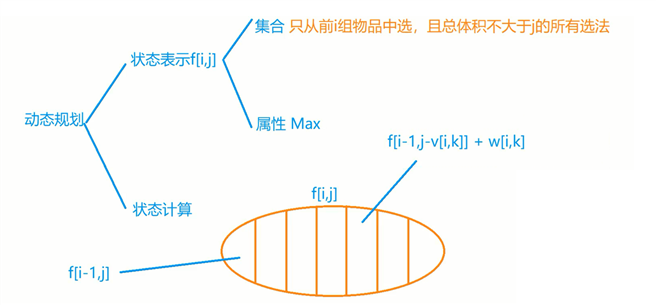
物品有N组,每组有若干个。每组最多只能选一个物品。
枚举第i组物品选哪个,可以分成不选第i组物品,第i组物品选第1个,第i组物品选第2个,……
题目链接:https://www.acwing.com/problem/content/description/9/
代码实现:
二维优化成一维时,如果用的是上一层的状态的话就从大到小来枚举体积,如果用的是本层的话就要从小到大来枚举体积。从大到小就可以保证我们使用的上一层状态还没被更新掉。
#include<iostream>
using namespace std;
const int N = 110;
int n,m;
int f[N];
int v[N][N],w[N][N],s[N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++)
{
cin >> s[i];
for(int j = 0; j < s[i]; j++)
cin >> v[i][j] >> w[i][j];
}
// 从前往后枚举所有物品
// 从大到小枚举所有体积
// 枚举所有的选择
// 如果第i组第k件物品体积<=j时才有更新他的必要
for(int i = 1; i <= n; i++)
for(int j = m; j >= 0; j--)
for(int k = 0; k < s[i]; k++)
if(v[i][k] <= j)
f[j] = max(f[j], f[j-v[i][k]] + w[i][k]);
cout << f[m] << endl;
}
原文:https://www.cnblogs.com/ApStar/p/14610118.html