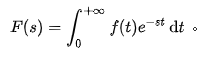Laplace和Z变换

1.拉普拉斯变换

s = a + jw;

拉普拉斯变换相当于原函数乘以一个指数的傅里叶变换， 如下

2. Z变换

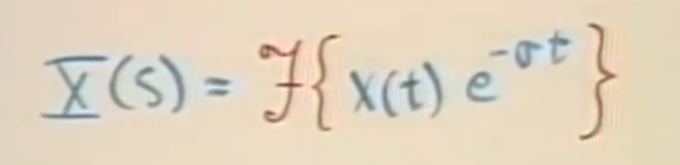
Z^n是一个eigen-function, 把所有的信号拆成 z^n.

证明如下. z^n经过一个系统后

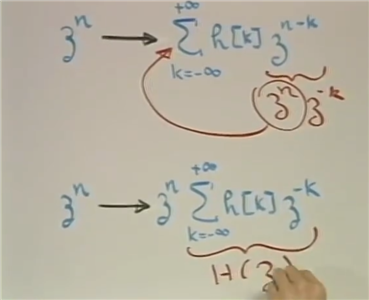
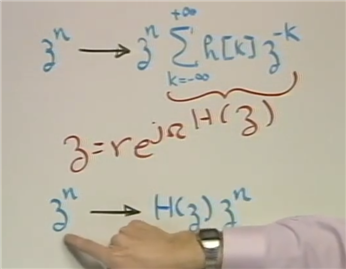
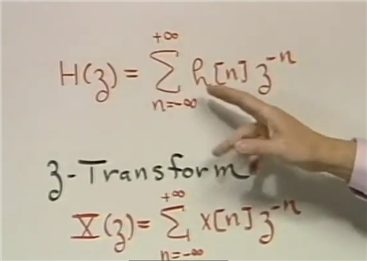
Z 变换公式

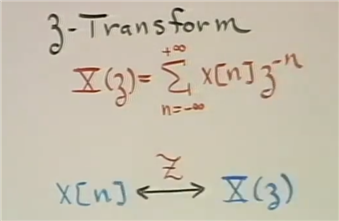
离散时间傅里叶变换和Z变换的比较

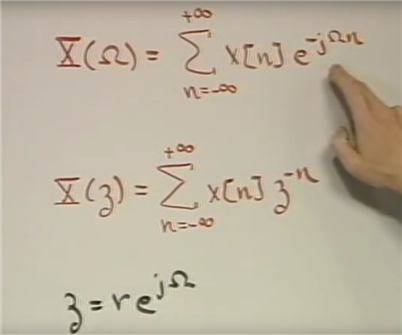
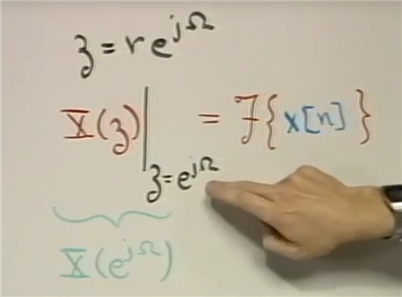
傅里叶变换融入到了Z变换里面

Z变换相当于原序列乘以r^(-n)后的傅里叶变换

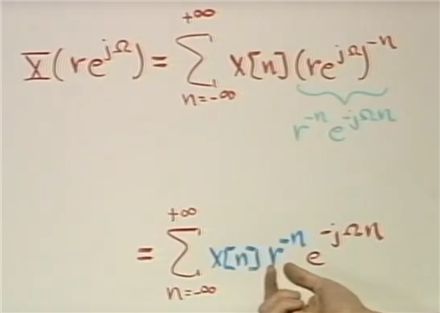
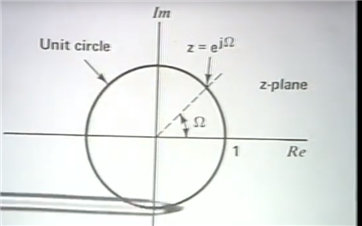
 单位元上面的点就是傅里叶变换, 因为r=1；uint

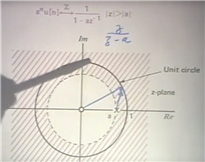
对于a^n * u[n]函数来说

求傅里叶变换的maginitude的大小

即 (z-0) 向量的模 除以 (z-a)向量的模 就得到了特定的傅里叶变换的magnitude的大小了

对于laplace 变换,是否收敛只取决与 s = a + jw, 其中的a, 所以laplace的收敛边界是垂直x轴的

对于z变换, 只取决与 z=r*e^jw 其中的r， 所以收敛边界是一个圆

right-sided 中心在右边, 左边某一点开始到负无穷值都为0 

left-sided的中心在左边, 

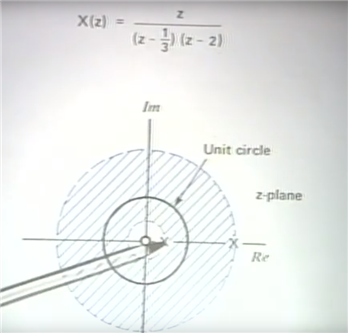
例子

逆Z变换

2pi的话 绕一圈就是2pi了。上式 两边乘以 r^(-n) 应该是能推导出来的.

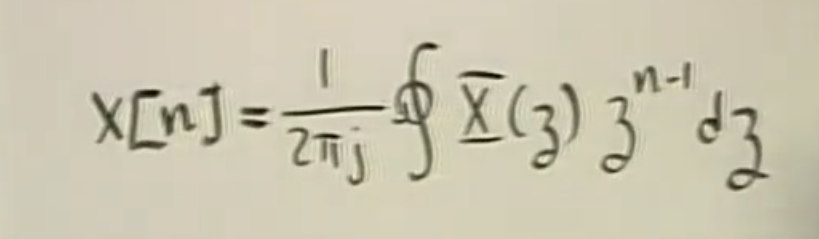
另外一种得到Z^n参数的方法, 拆开成 z^(-n)次方

 总结公式

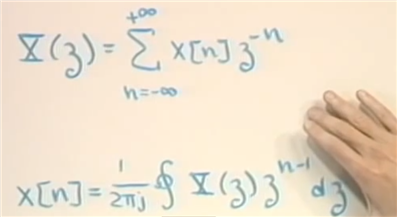
Z变换性质的推导。

Z变换的phase和模的大小

phase是以2pi为周期的函数，因为

z变换性质

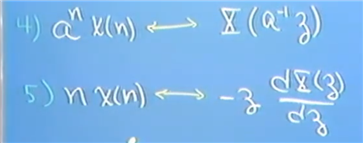
 定理2 证明

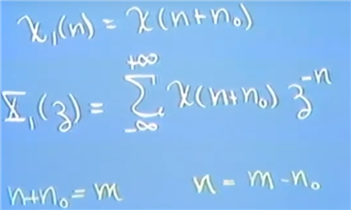
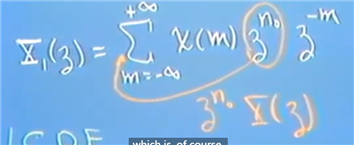
定理2的应用  Linear Constant Difference Equation

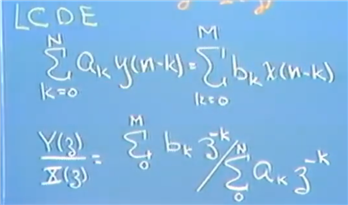
定理4的证明

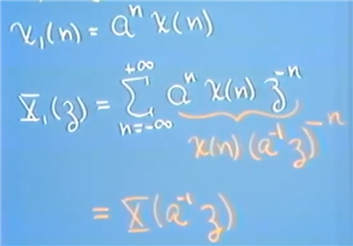
 定理4的应用：本来的zero或者pole 是Z0, 原函数乘以a^n后变成了aZ0；

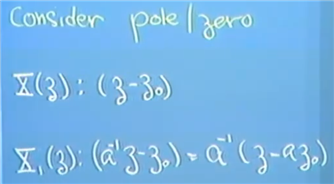
通过pole and zero 看magnitude的例子

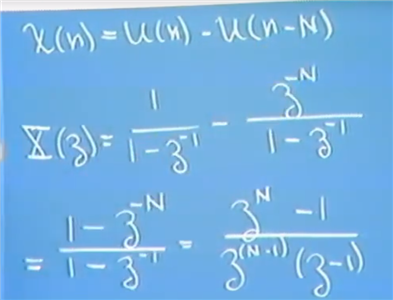
圈圈是zero

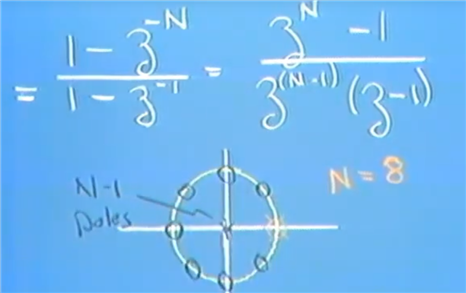
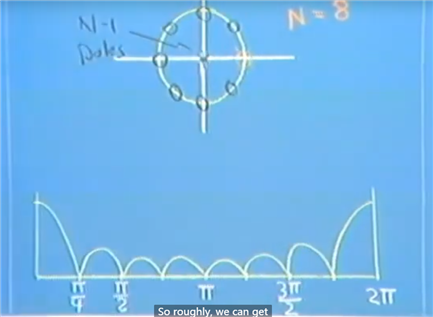
z变换后带z = e^jw进去,

Laplace和Z变换

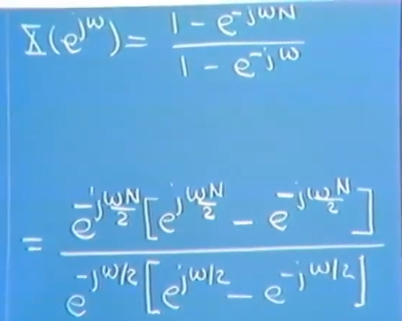
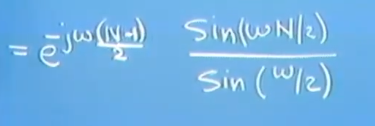
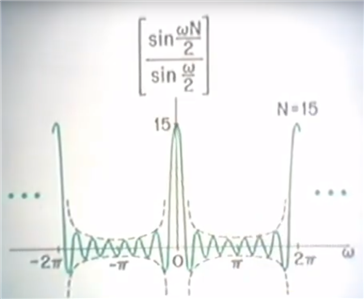
原文：https://www.cnblogs.com/robsann/p/14613492.html