回溯算法、把所有情况试一遍
需要填入数字的格,去掉不可能的数字,每一个可能的数字都要试
1、当填写第i行,第j列的元素时,需要知道其对应的行,列,块中,1-9数字的使用情况,从而选用不同的数字
新建row = [set(range(1, 10)) for _ in range(9)] 记录每一行可用的数字
col = [set(range(1, 10)) for _ in range(9)] 记录每一列可用的数字
block = [set(range(1, 10)) for _ in range(9)] 记录每一块可用的数字
2、if board[i][j] != ‘.‘ 碰到的是事先给好的数字,不需要咱们填,
那这个事先给好的数字不能出现在对应的行,列,块可用数字的集合当中
val = int(board[i][j])
row[i].remove(val)
col[j].remove(val)
block[(i // 3)*3 + j // 3].remove(val)
else 碰到的是空格,需要填入数字,把这个位置先记录下来
3、记录好了所用需要填数的空格和每一行每一列每一块可用的数。开始回溯
4、空格的索引,行列索引都好找
块的索引b = (i // 3)*3 + j // 3
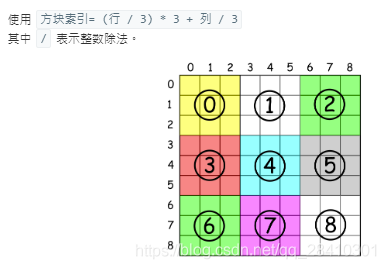
比如四行五列,就是第四块
5、一个一个试row col block中共同存在的数,这些数都是符合规定的
for val in row[i] & col[j] & block[b]:取交集
6、放入之后代表这个数就不能用了,把这个数在row col block中删掉
row[i].remove(val)
col[j].remove(val)
block[b].remove(val)
7、递归
8、递归完后把这个数再还回来,万一这个数导致后面的数独做不下去了,还能反悔
def solveSudoku(self, board: List[List[str]]) -> None: row = [set(range(1, 10)) for _ in range(9)] # 行剩余可用数字 col = [set(range(1, 10)) for _ in range(9)] # 列剩余可用数字 block = [set(range(1, 10)) for _ in range(9)] # 块剩余可用数字 empty = [] # 收集需填数位置 for i in range(9): for j in range(9): if board[i][j] != ‘.‘: # 更新可用数字 val = int(board[i][j]) row[i].remove(val) col[j].remove(val) block[(i // 3)*3 + j // 3].remove(val) else: empty.append((i, j)) def backtrack(iter=0): if iter == len(empty): # 处理完empty代表找到了答案 return True i, j = empty[iter] b = (i // 3)*3 + j // 3 for val in row[i] & col[j] & block[b]: row[i].remove(val) col[j].remove(val) block[b].remove(val) board[i][j] = str(val) if backtrack(iter+1): return True row[i].add(val) # 回溯 col[j].add(val) block[b].add(val) return False backtrack()
原文:https://www.cnblogs.com/zhaojiayu/p/14613846.html