定比分点坐标公式

前言

公式内容

在平面直角坐标系中，已知两点 \(A(x_1，y_1)\)，\(B(x_2，y_2)\)，过两点的直线上有一点 \(P\)，设其坐标为\(P(x，y)\)，

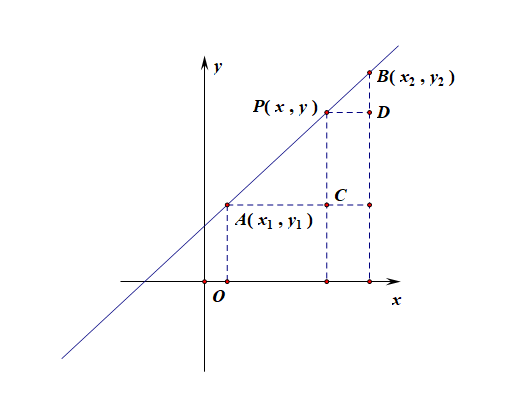
分别过点 \(A\)， \(P\)， \(B\)作坐标轴的垂线，可得交点 \(C(x，y_1)\)， \(D(x_2，y)\)，

由图可知， \(\triangle ACP\sim \triangle PDB\)，则有 \(\cfrac{AC}{PD}=\cfrac{PC}{BD}\)，[\(\cfrac{AC}{PD}=\cfrac{AP}{PB}\)]

即 \(\cfrac{x-x_1}{x_2-x}=\cfrac{y-y_1}{y_2-y}\)，

设此比值为\(\lambda\) ，则 \(\overrightarrow{AP}:\overrightarrow{PB}=\lambda\)，

则由\(\cfrac{x-x_1}{x_2-x}=\cfrac{y-y_1}{y_2-y}=\lambda\)，可以解得，

那么我们说点 \(P\) 分有向线段 \(\overrightarrow{AB}\) 的比为\(\lambda\)，称点 \(P\) 为定比分点，并将上式称为定比分点坐标公式。

当 \(P\) 为内分点时， \(\lambda>0\) ；当 \(P\) 为外分点时， \(\lambda<0(\lambda\neq -1)\) ；当 \(P\) 与 \(A\) 重合时， \(\lambda=0\) ；当 \(P\) 与 \(B\) 重合时， \(\lambda\) 不存在。

公式应用

【公式的应用之一：线段的中点坐标公式推导】当点 \(P\) 为线段 \(AB\) 的中点时，则 \(\lambda=1\) ，代入定比分点公式可得中点坐标公式：

【公式的应用之二：三角形重心坐标公式推导】若三角形的三个顶点坐标分别为\(A(x_1，y_1)\)，\(B(x_2，y_2)\)，\(C(x_3，y_3)\)，则其重心\(M(x_0，y_0)\)满足\(x_0=\cfrac{x_1+x_2+x_3}{3}\)，\(y_0=\cfrac{y_1+y_2+y_3}{3}\)，

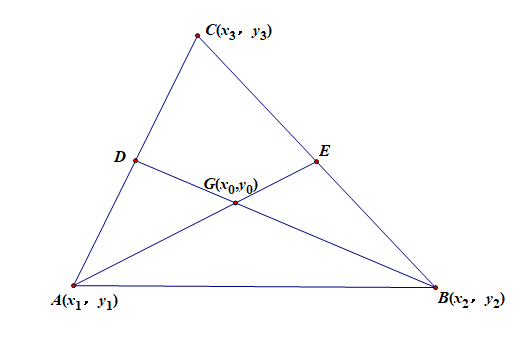
证明：如图所示，重心\(G\)在以\(BC\)为底边的中线\(AE\)上，则点\(E\)的横坐标\(x_E=\cfrac{1}{2}(x_2+x_3)\)，点\(E\)的纵坐标\(y_E=\cfrac{1}{2}(y_2+y_3)\)，且有\(EG=\cfrac{1}{2}AG\)，\(EG=\cfrac{1}{3}AE\)，

为使用定比分点坐标公式，梳理如下：

已知线段\(AE\)，且有\(A(x_1，y_1)\)，\(E(\cfrac{x_2+x_3}{2}，\cfrac{y_2+y_3}{2})\)，定比为\(\lambda=\cfrac{AG}{GE}=2\)，

则定比分点\(G\)即三角形的重心\(G(x_0，y_0)\)的坐标为：

\(x_0=\cfrac{x_1+\lambda x_E}{1+\lambda}=\cfrac{x_1+2\times \cfrac{x_2+x_3}{2}}{1+2}=\cfrac{x_1+x_2+x_3}{3}\)，

\(y_0=\cfrac{y_1+\lambda y_E}{1+\lambda}=\cfrac{y_1+2\times \cfrac{y_2+y_3}{2}}{1+2}=\cfrac{y_1+y_2+y_3}{3}\)；证毕。

典例剖析

【直线的参数方程之一形式】求直线 \(AB\) 的参数方程。

解析：在平面直角坐标系中，已知两点 \(A(x_1，y_1)\)，\(B(x_2，y_2)\)，在直线上任取一点 \(P\)，设其坐标为\(P(x，y)\)，

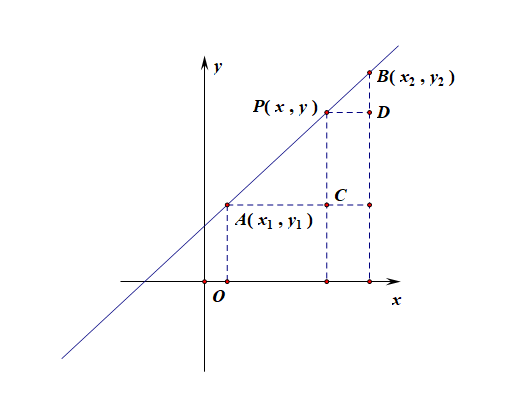
分别过点 \(A\)， \(P\)， \(B\)作坐标轴的垂线，可得交点 \(C(x，y_1)\)， \(D(x_2，y)\)，

由图可知， \(\triangle ACP\sim \triangle PDB\)，则有 \(\cfrac{AC}{PD}=\cfrac{PC}{BD}\)，[\(\cfrac{AC}{PD}=\cfrac{AP}{PB}\)]

即 \(\cfrac{x-x_1}{x_2-x}=\cfrac{y-y_1}{y_2-y}\)，

设此比值为\(\lambda\) ，则 \(\overrightarrow{AP}:\overrightarrow{PB}=\lambda\)，

则由\(\cfrac{x-x_1}{x_2-x}=\cfrac{y-y_1}{y_2-y}=\lambda\)，可以解得，

\(\left\{\begin{array}{l}{x=\cfrac{x_1+\lambda x_2}{1+\lambda}}\\{y=\cfrac{y_1+\lambda y_2}{1+\lambda}}，\end{array}\right.\) (\(\lambda\)为参数，\(\lambda\neq -1\)).

这就是经过两点 \(A(x_1，y_1)\)，\(B(x_2，y_2)\) 的直线的参数方程，其中参数 \(\lambda\) 的几何意义是点 \(P\) 分有向线段 \(\overrightarrow{AB}\) 的数量比 \(\cfrac{AP}{PB}\).

定比分点坐标公式

原文：https://www.cnblogs.com/wanghai0666/p/14616661.html