原码恢复余数法:
规则:将被除数-除数,
结果大于0,商1,余数左移一位。
结果小于0,商0,恢复余数,余数左移一位。
重复上述操作,直至商的精度满足要求为止。
本质上来说,不恢复余数法是只是为了在计算的时候能够不判断除数和余数的大小而规定的一种算法,每一次只需要先减就是了,减完了以后,再通过双符号位判断上商为0还是1,然后再判断是否要恢复余数
参考链接:考研计组 | 原码(不)恢复余数除法、补码不恢复余数除法_?ideal world?~ヽ(?︺?)Hi-CSDN博客_不恢复余数法
原码不恢复余数法:
与恢复余数法的区别:
若余数(被除数)为负,表示不够减,商上0,恢复余数(加上除数) ,左移一位,加上[-y]_补 , 加上[ y ] 补 [y]_补[y] 链接同上
?
补码除法:

例子:(必须满足被除数绝对值小于除数绝对值)
x / y = + 0.1000 / (-0.1010) = ?
R = X[补] = 00 1000 B=Y[补] = 110110 -B = 001010 商Q= 00000
步骤:
因为余数在每次运算后都要被不断置为被除数,所以初始化r = X【补】
第一步:
当前余数是正数,是双符号位,而Y的补码是负号,所以需要上商为0,然后向左移动余数和商各一位,因为是补码的双符号位移位, 其中,余数最高位移动到第二符号位,商的最高位移动到余数最低位,然后进行+B的操作
得到 R = 01 0000 + 11 0110 = 1 000110 然后将 被除数赋值给余数 得到 r = 000110 Q = 00000
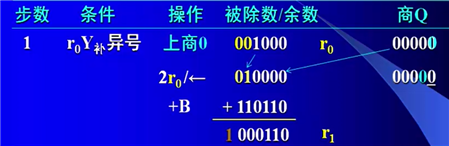
第二步:
当前除数和r1异号,因此在Q末尾上0, 然后向左移动余数和商各一位, 其中,余数最高位移动到第二符号位,商的最高位移动到余数最低位,然后进行+B的操作
得到R = 001100 + 110110 = 1 000010 然后将 被除数赋值给余数 得到 r = 000010 Q = 00000

第三步:
同上,商继续上0 ,基本操作同上:得
R = 111 010 商 Q = 00000

第四步:
因为余数和y补同号, 所以上商1 ,然后整体左移一位,按照之前的规则上位,并且-B(相当于+【-B】补码)
得 余数 = 111110, 商Q = 00010

除数的位数只有四位,因此循环完成:
商校正:商的最高位+1(取反),最低位置1, 最终得到 Q = 10010
余数校正:余数在运算过程中左移了四位,因此需要将其缩小到原来的 2^(-4), 最终得到r = 2^(-4) * r4
原文:https://www.cnblogs.com/SValley/p/14618578.html