作者:elfin 资料来源:torch.nn.LSTM
? 在传统的统计学中,有一门专门介绍时间序列的课程。其主要研究事件的发生与时间(可以是广义的)有较强的关联,这时传统机器学习算法并不能很好地解决这种带有时序的数据预测、特征挖掘。随着深度学习的火爆,从AR到RNN,再到LSTM及其变种,关于序列特征的挖掘取得了很大的进步。
RNN的结构如下:
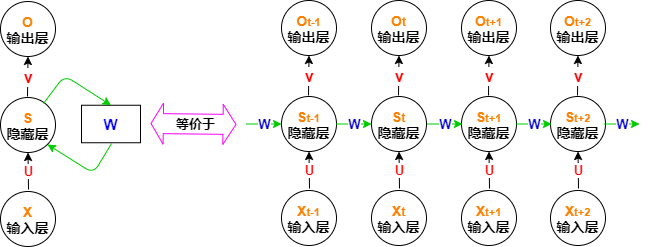
注意这里的参数是共享的,即\(W, U, V\)只有一份,不会随着单元数的增加而增加。
关于隐藏层与输出层的公式为:
从上式可以发现输出只与当前的隐藏层及其输出权值矩阵\(V\)有关;但是隐藏层不仅与当前输入\(X\)有关,还与上一个单元的隐藏层有关。这与\(AR:X_{t}=\lambda X_{t-1} + \varepsilon_{t}\),非常类似,传统的AR模型在RNN中主要对应了隐状态\(S\)的传递,而RNN模型的隐含层相对于传统自回归模型添加了当前输入的调制,以及当前输出是对历史信号+当前调制信号的再调制。有一点我们会发现:传统的自回归模型,它能够调制\(q\)阶信号(最近的\(q\)个历史节点),但是RNN只是当前与最后一个节点,这对于长距离依赖肯定是不好的。
关于RNN有如下的问题:
? 为什么要开发这类 LSTM-style 模型?如上述RNN缺点:RNN模型无法解决长期依赖(长距离依赖)问题,但是序列模型的一个重要特点就是具有长期依赖。如文字序列的上下文、最近一段时间的天气、股票等等。LSTM的提出就是为了解决这个问题!
? LSTM解决问题的关键点在于门限(gates,亦称门)技术。它有三个门,分别为:遗忘门、输入门、输出门。
三种门的简单介绍:
输入门
输入门的作用是对输入的信号进行调制,那么它是如何调制的呢?调制对象、调制量分别是什么?
首先,调制对象是当前的输入信号与上一个节点单元的输出信号:\(\left [ h_{t-1},x_{t} \right ]\);
其次,调制量是\(W_{i}, W_{C}\),由如下的公式我们可以获得更新量、更新对象:
输入门的可视化:
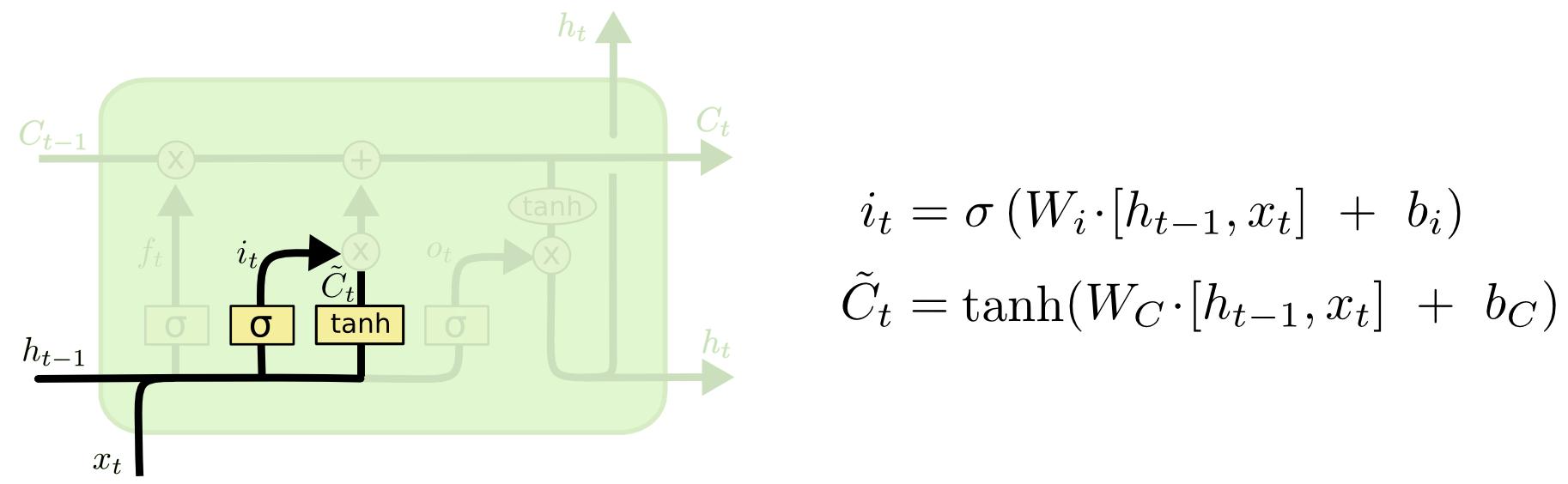
注:图片来源于http://colah.github.io/posts/2015-08-Understanding-LSTMs/
将更新值 \(i_{t}\) 与候选值 \(\tilde{C}_{t}\) 相乘即得到输入门的 “输入”。
遗忘门
遗忘门的可视化:
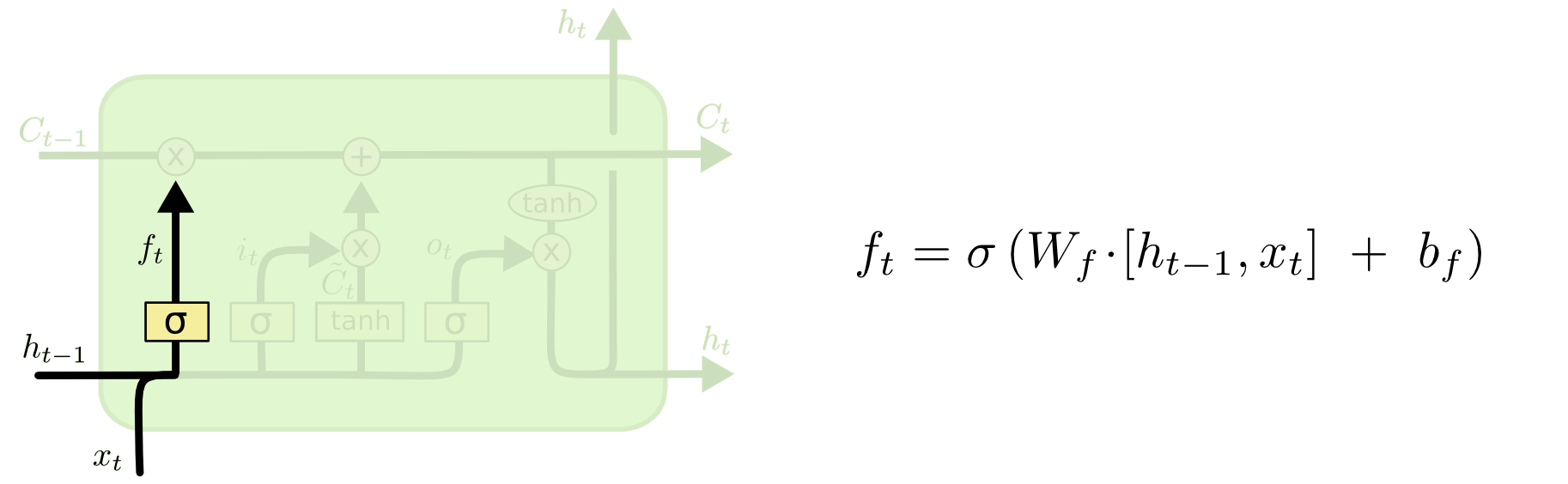
遗忘门是对历史信息的调制。那么它又是如何调制信号的呢?
首先,调制的对象是细胞状态\(C_{t-1}\)(历史信息);
其次,调制量是\(W_{f}\),由调制量得到当前节点的遗忘值:
细胞状态更新:
将遗忘值乘以上一时刻的细胞状态得到当前细胞单元要使用的历史信息,再加上输出门的调制信息,得到当前的细胞状态\(C_{t}\),即:
状态更新可视化:
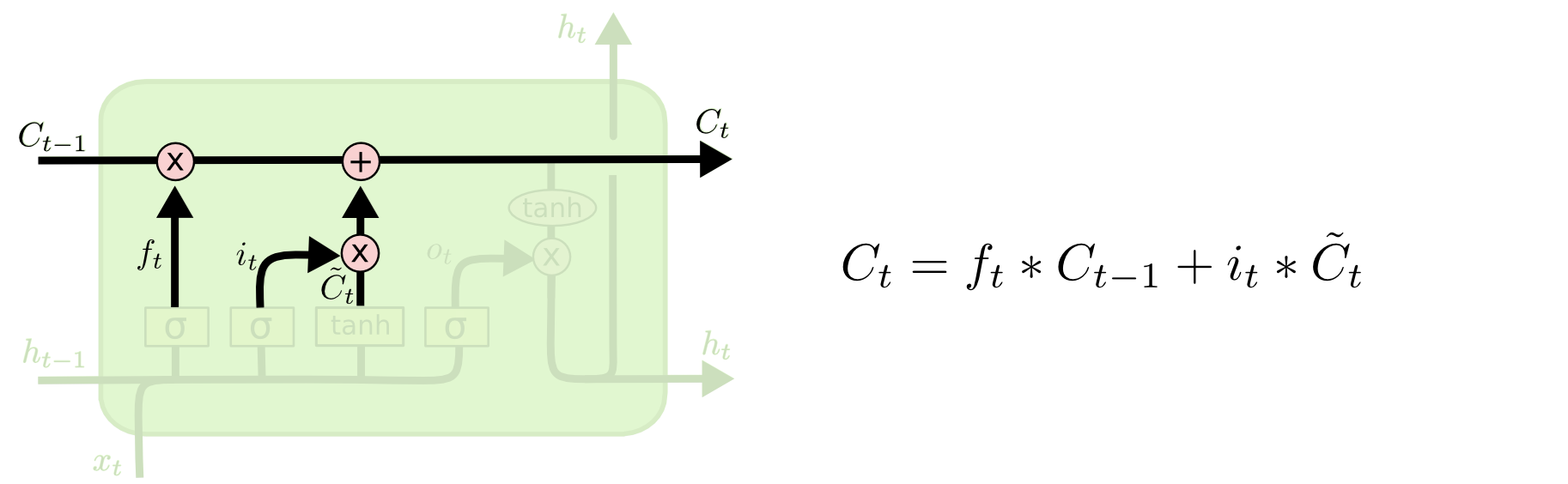
输出门
输出门是调制信号得到输出信息的门。
首先,由输入对象加上一时刻输出组合 \(\left [ h_{t-1},x_{t} \right ]\) 获取输出候选;
其次,由当前细胞状态\(C_{t}\)使用tanh激活获取输出更新权值,具体公式如下:
输出门可视化:
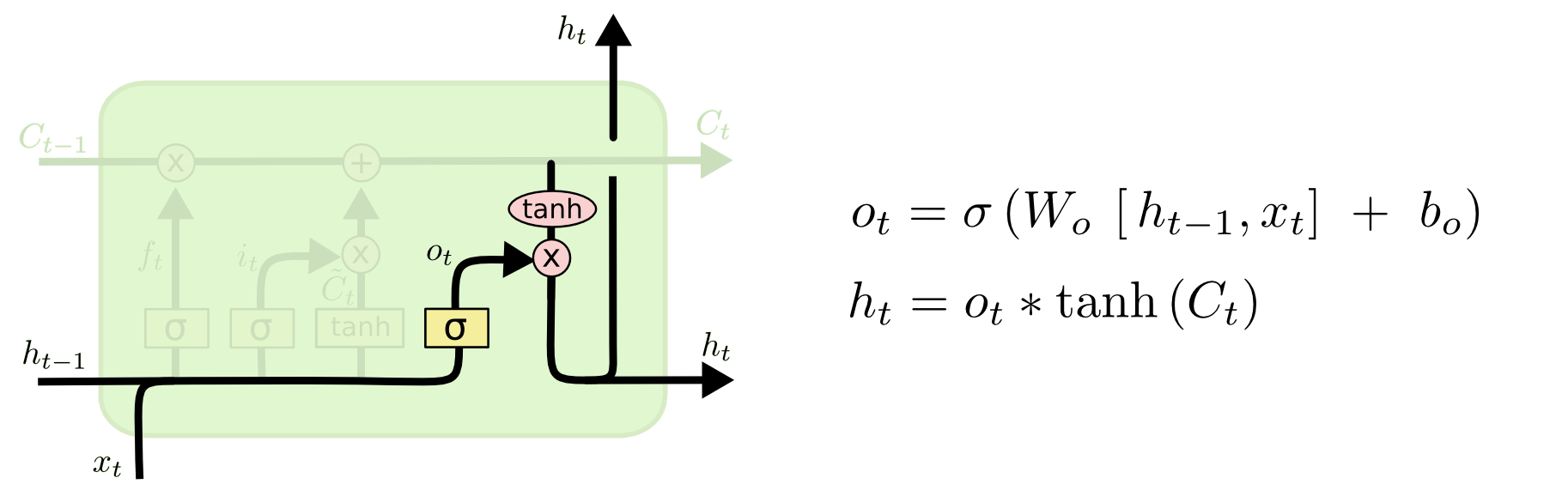
小结:LSTM的计算公式:
? LSTM加入了门对历史信息、上个节点的输出、当前节点的输入信息进行调制,相当于对历史信息、当前输入都是有选择地接收处理而不是全盘吸收,有点局部注意力的感觉。注意这里的参数仍然是不随节点的变化而变换的,但是由于门的存在,抵消了硬值对信息的损坏。
因为对历史信息的保留及调制,一定程度上可以将其看作在长期依赖上的改进,但是LSTM仍然有一些缺点:
这个类是对输入序列应用多层长短时记忆(LSTM)RNN。
根据第2章,我们已经知道了单层LSTM的参数计算公式,在pytorch中,类似的计算公式为:
其中:
对于一个多层LSTM,第\(l(l\geq 2)\)层的输入\(x^{(l)}_t\)是前一层对应节点的隐状态\(h^{(l-1)}_t\)乘以dropout变量:\(\delta^{(l-1)}_t\),其中\(\delta^{(l-1)}_t\)是Bernoulli随机变量,这里的dropout的概率为\(0\)。
注意:bidirectional=True 并不是等价于 num_layers=2
LSTM的输入有 input 、h_0、c_0
torch.nn.utils.rnn.pack_padded_sequence()或torch.nn.utils.rnn.pack_sequence()如果(h_0, c_0)没有提供,默认为0。
LSTM的输出有output、h_n、c_n
output的shape为 (seq_len, batch, num_directions * hidden_size) ,即最后一层每个时刻\(t\)的隐状态h_t,即(h_1, **h_2 **, \(\cdots\), h_n);
如果input中给了torch.nn.utils.rnn.PackedSequence ,output也将成为packed sequence。
h_n的shape为 (num_layers * num_directions, batch, hidden_size) ;
c_n的shape为 (num_layers * num_directions, batch, hidden_size) 。
LSTM.weight_ih_l[k]
第\(k\)层输入\(x\)对应的权值 (W_ii|W_if|W_ig|W_io) ,当k = 0时shape为 (4*hidden_size, input_size),否则为 (4*hidden_size, num_directions * hidden_size)。
LSTM.weight_hh_l[k]
第\(k\)层隐状态\(h_{t}\)对应的权值 (W_hi|W_hf|W_hg|W_ho),shape为 (4*hidden_size, hidden_size)。
LSTM.bias_ih_l[k]
第\(k\)层输入的偏置 (b_ii|b_if|b_ig|b_io) ,shape为 (4*hidden_size)。
LSTM.bias_hh_l[k]
第\(k\)层隐状态的偏置 (b_hi|b_hf|b_hg|b_ho),shape为 (4*hidden_size)。
所有权值、偏置的初始化都是使用均匀分布:\(U(-\sqrt{k},\sqrt{k})\),其中\(k = \frac{1}{hidden\_size}\)
如果下面的条件都满足:
torch.float16;则,persistent算法可用于提高性能。
# 官方案例
>>> rnn = nn.LSTM(10, 20, 2)
>>> input = torch.randn(5, 3, 10)
>>> h0 = torch.randn(2, 3, 20)
>>> c0 = torch.randn(2, 3, 20)
>>> output, (hn, cn) = rnn(input, (h0, c0))
>>> type(output)
Out[9]: torch.Tensor
>>> output.shape
Out[10]: torch.Size([5, 3, 20])
>>> input0 = torch.randn(15, 3, 10)
>>> output, (hn, cn) = rnn(input0, (h0, c0))
>>> output.shape
Out[11]: torch.Size([15, 3, 20])
# 注意这里的3是batch,15是seq的长度。也即序列是可变长的,输出的序列单元数是和输入进行匹配的。
参考文献:
待更……
原文:https://www.cnblogs.com/dan-baishucaizi/p/14628897.html