Leetcode-灯泡开关

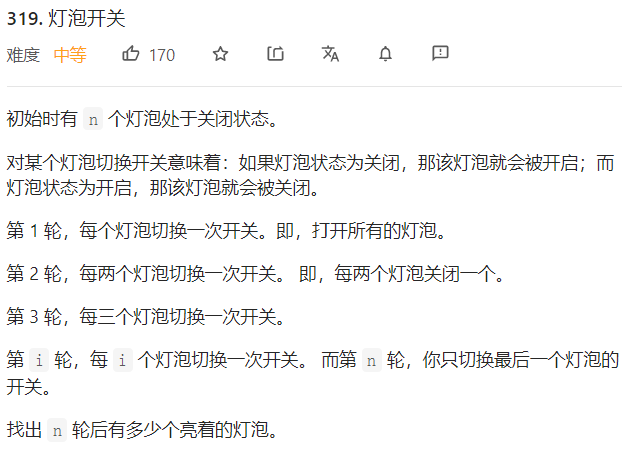
 最先开始想模拟开关过程，结果运行时结果出错，但是发现错得很有规律，就手动模拟了一次，才发现数学规律简单至极，就是开平方。

分析

分析过程得画图，这里引用一个答主的解答。

模拟一下n从1到12的过程。第一轮打开了12个灯泡：

 不用关心大于n的灯泡，用黑框表示。

列出n从1-12的过程中所有的灯泡示意图。

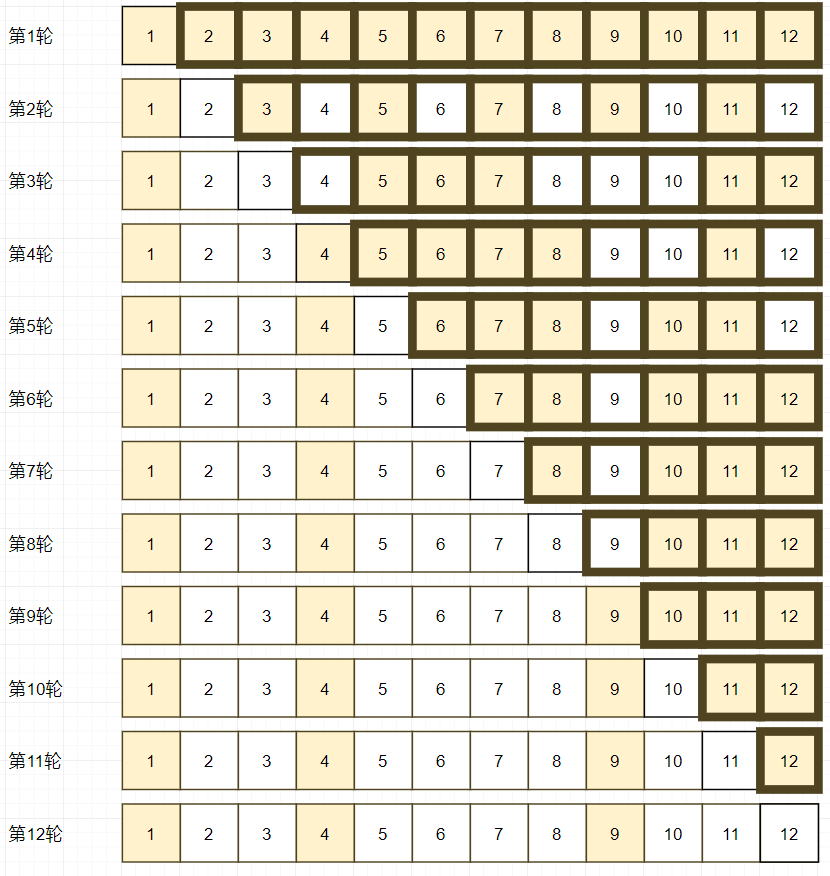
列表如下：

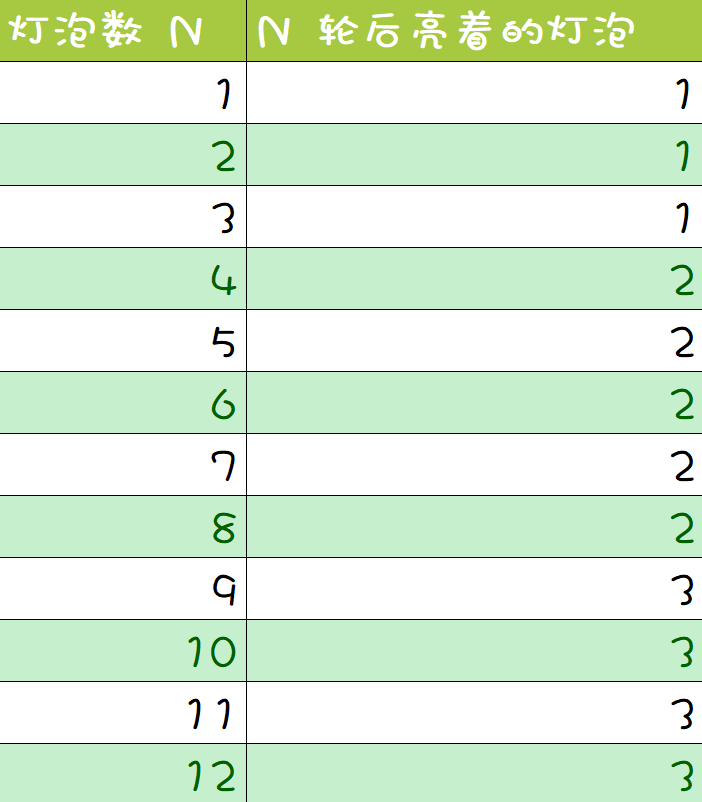
 证明：

约数，又称因数。整数a除以整数b(b≠0) 除得的商正好是整数而没有余数，我们就说a能被b整除，或b能整除a。a称为b的倍数，b称为a的约数。

从我们观察可以发现，如果一个灯泡有奇数个约数，那么最后这个灯泡一定会亮着。

奇数（odd）指不能被2整除的整数 ，数学表达形式为：2k+1， 奇数可以分为正奇数和负奇数。

所以其实我们是求，从1-n有多少个数的约数有奇数个。而**有奇数个约数的数一定是完全平方数。**这是因为，对于数n，如果m是它的约数，则n/m也是它的约数，若m≠n/m，则它的约数是以m、n/m的形式成对出现的。而m＝n/m成立且n/m是正整数时，n是完全平方数,而它有奇数个约数。

再次转化问题，求1-n有多少个数是完全平方数。

代码实现

1 class Solution {
2     public int bulbSwitch(int n) {
3         return (int)Math.sqrt(n));
4     }
5 }

图表来源：

作者：ivan1
链接：https://leetcode-cn.com/problems/bulb-switcher/solution/bu-jiu-shi-qiu-ping-fang-gen-ma-by-ivan1/

Leetcode-灯泡开关

原文：https://www.cnblogs.com/pycdu/p/14631537.html