LeetCode-地下城游戏（反向动态规划）

 做这道题的时候首先反应是用动态规划来解，核心思想是让 从出发点到当前点的路径和 尽可能大的同时 从出发点到当前点所需的最小初始值 尽可能小。

结果实现的时候发现两者矛盾了，两个同样参数同时影响后续决策，不满足无后效性。

按道理来说这个时候就该考虑换个角度做了，奈何做的题少，没见识，再加上头铁，就想莽过去。硬写了个暴力剪枝的算法，虽然做出来了但性能差的离谱。

实在凹不出来看题解，才发现可以反向动态规划，让公主去救骑士。恍然大悟。

思路

这里引用一个答主的题解：

1、为啥用反向？因为要正向更新dp无法更新当前所需最小的生命值
2、反向更新dp：用负数记录，负数的相反数表示从此处走到右下角所需要扣的血量的最小值，即所需的最低初始健康点数-1
3、更新状态分两步：(我用的是负数进行更新，但从其相反数进行理解)
　　dungeon[i][j] = dungeon[i][j] + Math.max(dungeon[i + 1][j], dungeon[i][j + 1]);
　　取下一步的所需要扣的血量的最小值(负数用max)与此处的数值的和
　　if (dungeon[i][j] > 0) dungeon[i][j] = 0;
　　所需要扣的血量的最小值最小为零，不可能为负数 (指该处数值的相反数)
4、总的状态转移方程：dp[i][j]=max(min(dp[i+1][j],dp[i][j+1])+dungeon(i,j),1)

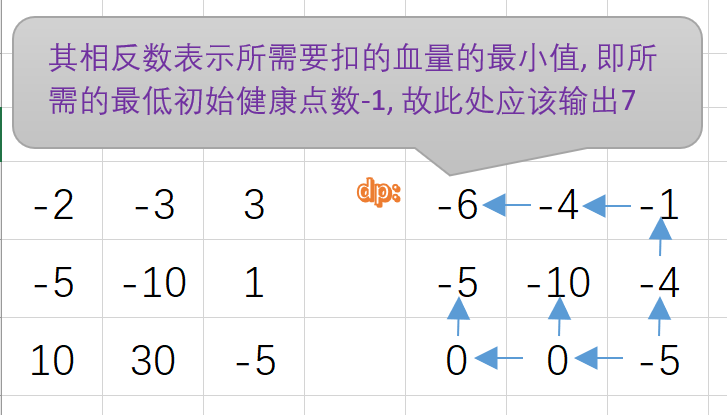
作者：quantum-10
链接：https://leetcode-cn.com/problems/dungeon-game/solution/fan-xiang-dp-wen-zi-de-kan-bu-ming-bai-jiu-lai-kan/

代码实现

在这个答主代码的基础上，改良了一下数组使用，降低了内存消耗。

 1 class Solution {
 2     public int calculateMinimumHP(int[][] dungeon) {
 3         int row = dungeon.length;
 4         int col = dungeon[0].length;
 5         int dp[] = new int[col];
 6         for (int i = row - 1; i >= 0; i--) {
 7             for (int j = col - 1; j >= 0; j--) {
 8                 if (i == row - 1 && j == col - 1) dp[j] = Math.max(1, 1 - dungeon[i][j]);
 9                 else if (i == row - 1 && j != col - 1) dp[j] = Math.max(1, dp[j + 1] - dungeon[i][j]);
10                 else if (i != row - 1 && j == col - 1) dp[j] = Math.max(1, dp[j] - dungeon[i][j]);
11                 else dp[j] = Math.max(1, Math.min(dp[j], dp[j + 1]) - dungeon[i][j]);
12             }
13         }
14         return dp[0];
15     }
16 }

使用语言：java

最近做的leetcode有意思的都记录完了，下次攒够一波题再来做记录。

LeetCode-地下城游戏（反向动态规划）

原文：https://www.cnblogs.com/pycdu/p/14636328.html