问题:
给定n个初始状态为off的灯,
求最后on的灯共有几个。
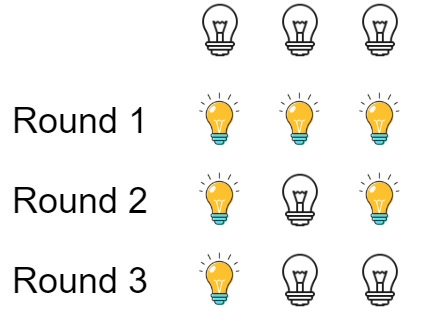
Example 1: Input: n = 3 Output: 1 Explanation: At first, the three bulbs are [off, off, off]. After the first round, the three bulbs are [on, on, on]. After the second round, the three bulbs are [on, off, on]. After the third round, the three bulbs are [on, off, off]. So you should return 1 because there is only one bulb is on. Example 2: Input: n = 0 Output: 0 Example 3: Input: n = 1 Output: 1 Constraints: 0 <= n <= 10^9
解法:math
根据题意:
我们观察:第n号灯,被按下开关的次数=
第 n的因数 轮。
ex:
这样有一个规律,
对于开关的特性:
那么我们要求的就是,存在奇数个因数的灯的个数。
即n以内,有多少个平方数。
sqrt(n);
n的平方根是多少,那么从1~这个平方根,有多少个数,就存在多少个n以内的平方数。
代码参考:
1 class Solution { 2 public: 3 int bulbSwitch(int n) { 4 return (int)sqrt(n); 5 } 6 };
原文:https://www.cnblogs.com/habibah-chang/p/14636712.html