象群游牧算法的数学模型

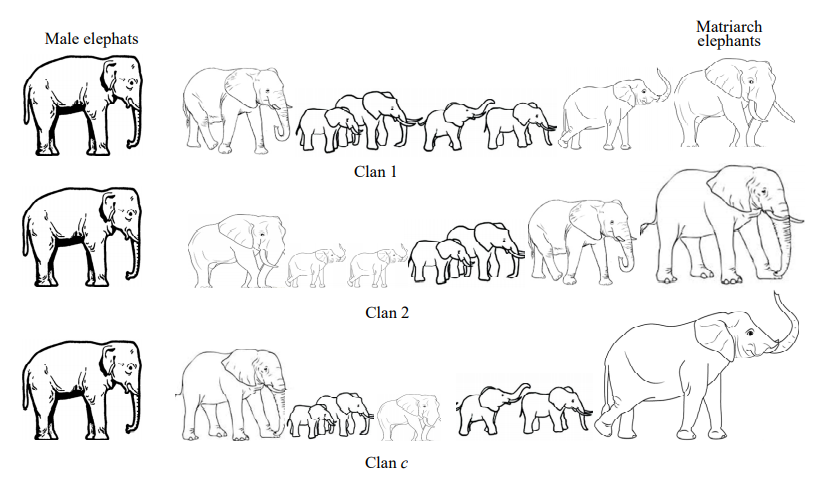
象群的游牧行为非常复杂，但是其中一些行为可以帮助我们寻找全局最优解和局部最优解。对此，进行数学建模为：
(1) 象群的每个部落都有固定数目的大象；
(2) 每次迭代中，部落中都有一定数目的大象离开部落，独自生活并与部落保持一定的联系；
(3) 每个部落都是由女族长领导-----在算法中，女族长是适应度值最大的大象。

象群游牧算法

部落中大象位置的更新公式

1）部落中普通大象的更新公式：

\(p_{jc}^{t+1} = p_{jc}^{t} + \alpha*(p_{best}-p_{jc}^{t})*rand\)
其中，\(p_{jc}^{t+1}\)和\(p_{jc}^{t}\)分别是部落\(c\)中，第\(j\)个大象的更新后和更新前的位置，\(t\)表示迭代次数，\(\alpha\)表示[0,1]之间的随机数。

2）族长的位置更新公式：

\(p_{center, c} = \frac{\sum_{r=1}^{n_c}p_{jc}^{t}}{n_c}\)
其中，\(n_c\)是部落中大象的数目。
\(p_{bested} = \beta*p_{center, c}\)
其中，\(p_{bested}\)表示更新后的族长位置, \(\beta\)是[0,1]的随机数。

3）公象的分离公式：

\(p_{worst}^{t+1} = p_{min,c} + rand*(p_{max,c} - p_{min,c})\)
其中，\(p_{max,c}\)和\(p_{min,c}\)表示部落中大象位置的上下界。

象群游牧Matlab代码

适应度函数

function z=chaffer(x)%chaffer函数x=(0...0) f(x)=0 x[-10,10]%%没测
n=10;
s1=0;
for i=1:n
s1=s1+x(i)^2;
end
z=((sin(sqrt(s1)))^2-0.5)/(1+0.001*s1)+0.5;
end

主函数

% ----------------------------------------------------------
% Title: Elephant Herbing Optimization Algorithm
% Institution: XI‘AN POLYTECHNIC UNIVERSITY
% Author: Liwenchao
% Time: 2020-11-8
% ----------------------------------------------------------
clc
clear
% ----------------------------
% Definition of Problems
% ----------------------------

CostFunction = @(x) chaffer(x); % cost function
dim_Var = 10; % variables of dimensions
VarMin = -32.768; % lower boundary
VarMax = 32.768; % upper boundary

% -------------------------------------------------------------------------
% Setting Parameters of Elephant Herbing Optimization Algorithm
% -------------------------------------------------------------------------

alpha = 0.75; % alpha is a scale factor that determines the influence of matriarch on elephant
beta = 0.01; % beta is a scale factor that determines the influence of the center of clan on elephant
epoches = 1000; % the maximum number of epoches
num_clan = 5; % the number of clans
num_pop = 10; % the number of elephants in each clans
num_male = 1; % leave family group

% -----------------------------------
% Initialization of Population
% -----------------------------------

init_pop = VarMin + rand(num_clannum_pop, dim_Var) . (VarMax - VarMin);
pop_fitness = zeros(num_pop, 1);
fit_clan = zeros(num_pop, 1);
pop_best_fitness = zeros(epoches, 1);

for n=1: num_clan*num_pop
pop_fitness(n) = CostFunction(init_pop(n, ??);
end
[pop_fbest, pop_best_loc] = min(pop_fitness);
best_pop = init_pop(pop_best_loc, ??;

%------------------------------------------
% EHO generation starts ......
%------------------------------------------
for iter=1:epoches
for j=1: num_clan
clan = init_pop((j-1)num_pop +1: j * num_pop, ??;
for k=1: num_pop
fit_clan(k,:) = CostFunction(clan(k, ??);
end
% best fitness value and its location
[fbest, best_loc] = min(fit_clan);
clan_best = clan(best_loc, ??;
% worst fitness value and its location
[fworst, worst_loc] = max(fit_clan);
clan_worst = clan(worst_loc, ??;
for k=1:num_pop
if any((k_{=best_loc)&(k}=worst_loc))
% update elephant position in clan except best and worst elephant
clan(k, ?? = clan(k, ?? + alpha(clan_best - clan(k, ??)rand;
elseif k==best_loc
% update leader or matriarch
clan_center = sum(clan) / num_pop;
clan(k, ?? = betaclan_center;
elseif k==worst_loc
% update worst elephant or male
clan(k, ?? = VarMin + rand* (VarMax - VarMin + 1);
end
init_pop((j-1)num_pop +1: j * num_pop, ?? = clan;
end
end
% ----------------------------------------------------------------
% evaluation population by the newly updated positions
% ----------------------------------------------------------------
for n=1: num_clannum_pop
pop_fitness(n) = CostFunction(init_pop(n, ??);
end
[new_pop_fbest, new_pop_best_loc] = min(pop_fitness);
if new_pop_fbest<pop_fbest
pop_fbest = new_pop_fbest;
pop_best_loc = new_pop_best_loc;
init_pop(pop_best_loc, ?? = init_pop(new_pop_best_loc, ??;
end
pop_best_fitness(iter, ?? = pop_fbest;
disp([‘Iteration ‘ num2str(iter) ‘: Best Cost = ‘ num2str(pop_fbest)]);
disp(init_pop(pop_best_loc, ??);
end
% -------------------------------------
% visualization
% -------------------------------------
figure;
%plot(pop_best_fitness)
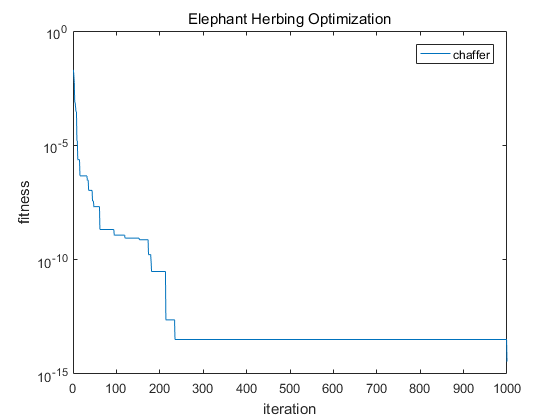
semilogy(pop_best_fitness);
xlabel(‘iteration‘);
ylabel(‘fitness‘);
legend(‘chaffer‘);
title(‘Elephant Herbing Optimization‘)

可视化

象群游牧算法--EHO

原文：https://www.cnblogs.com/mysterygust/p/14639356.html