几何题 正方形内弦图

Q: $\Box ABCD$ 中取一点 $E$ 使 $AE\bot EB,AE=1,CE=5 $ 求DE的长

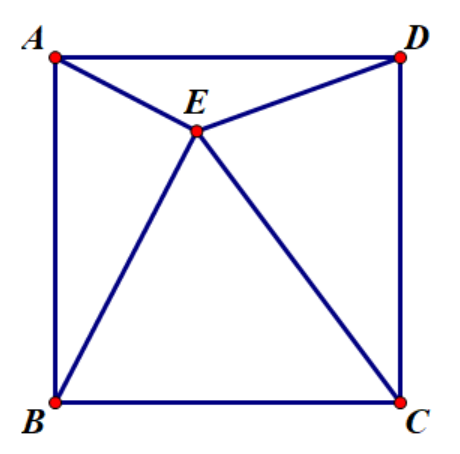
A:作如图

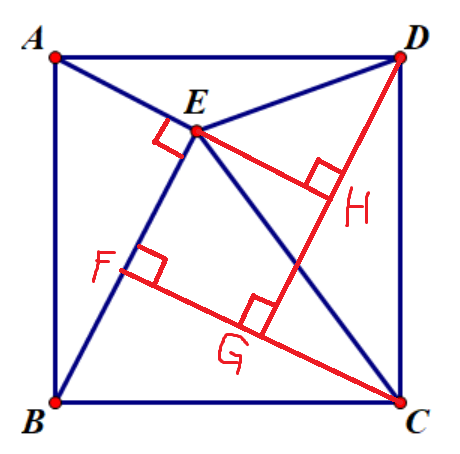
显然 $\triangle ABE\cong \triangle BCF\cong \triangle CDG\cong \triangle DAH$

则 $AE=BF=CG=DH=1$

设 $EF=FG=GH=HE=x$

根据勾股定理

 $EF^2+FC^2=EC^2$

 $x^2+(1+x)^2=25$

$x_1=3,x_2=-4$ ( $x_2$ 舍)

 $EH^2+HD^2=DE^2$
 $x^2+1=DE^2$
 $DE^2=10$
 $DE=\sqrt{10}$

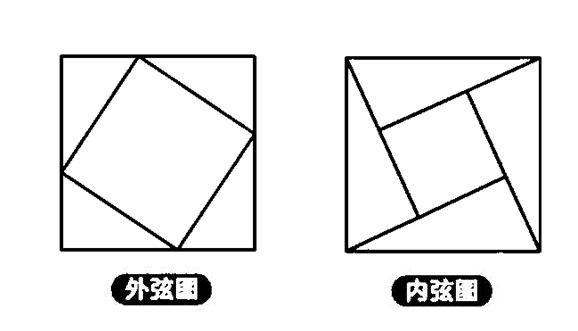
此类图称为正方形的内弦图

几何题 正方形内弦图

原文：https://www.cnblogs.com/zhangshaojia/p/14640690.html