高精度专题之乘法（大数乘法）

描述

输入两个高精度正整数M和N（M和N均小于100位）。求这两个高精度数的积。

格式

输入格式

输入两个高精度正整数M和N。

输出格式

求这两个高精度数的积。

输入样例

36
3

输出样例

108

限制

时间限制: 1000 ms

内存限制: 65536 KB

解题答案：

#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <algorithm>
using namespace std;
int a[210];
int b[210];
int c[10010];
int la,lb,lc;
int main()
{
    string M,N;
    cin>>M>>N;
    la=M.size();
    lb=N.size();
    for(int i=0;i<la;++i)
    {//字符反转
        a[i]=M[la-i-1]-‘0‘;
    }
    for(int i=0;i<lb;++i)
    {
        b[i]=N[lb-i-1]-‘0‘;
    }
    for(int j=0;j<la;++j)
    {
        for(int i=0;i<lb;++i)
        {//关键代码
            c[i+j]+=b[i]*a[j];
            c[i+j+1]+=c[i+j]/10;
            c[i+j]%=10;
        }
    }lc=la+lb;//3位数乘以2位数，最多为5位数
    while(c[lc]==0)lc--;//去0
    for(int i=lc;i>=0;--i)
    {
        printf("%d",c[i]);
    }
    return 0;
}

解析

在高精度乘法中，我们首先考虑是不是可以采用加法解决，比如3**2这样的计算，只需要将3自加两次就可，看似可以将其做成高精度加法的形式，但实则这样是不行的，比如123445985135681231165*5625269845626852,这样的计算，明显就吃不下了。

于是采用模拟的思维，用字符串和数组来处理，来看看我们平时是如何处理乘法的。

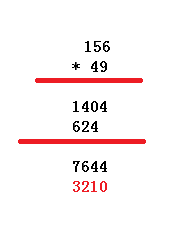
如上图：在上图中我们举了一个例子：采用15649，在现实中，我们遇到该运算，我们会首先把9与6相乘，然后把多出来的5来加上59，把个位上的4放在个位上，如果把9所在数组的位置为0，6所在的数组位置也为0，那么4所在的位置也是0，同理95+5是的到50，0放在了十位上，这是9对应的0位置没变，但5的位置变成了1，这是0也在数组的1位上，一次进行，4在2的位置上，由9的位置加上1的位置，所以我们得出c[j+i]=a[i]b[j]的表达式，然后就是相应的91+5满足了大于等于10的条件，则采取相应的进位操作， c[i+j+1]+=c[i+j]/10;和 c[i+j]%=10;最后把数字相加，这也是为什么是c[i+j]+=b[i]a[j]，而不是c[j+i]=a[i]*b[j]的原因.

高精度专题之乘法（大数乘法）

原文：https://www.cnblogs.com/5-StarrySky/p/14642053.html