题目描述
The National Road Service (NRS) wanted to make some changes to make sure that people are correctly ocially distancing from each other. However, NRS does not have the manpower to keep tabs on everyone. So, NRS wants to close down as many roads as possible while maintaining the connectivity between cities.
All of the roads in the existing road network are bi-directional roads connecting pairs of cities such that it is possible to travel between any pair of cities. NRS has taken a survey on roads, and come up with a priority ranking for each. The higher the priority score of a road, the more people can be on that road.
Normally, NRS would like to keep the higher priority roads. However, the NRS Director loves even numbers. This means that he wants to maximize the number of roads with an even priority score. Of all of these possible options, he wants to maximize the overall sum of priority scores of the roads selected.
The Problem
Given a network of roads, of all subsets of roads of minimum size that keep the whole network connected, determine the maximum sum of priority scores of the roads selected subject to the constraint of maximizing the number of roads chosen that have an even priority score.
输入
The first line will have a positive integer, n (n ≤ 100) with the number of road networks to be tested. The n test cases follow. The first line of each test case will have two integers, c (2 ≤ c ≤ 1,000) and r (c-1 ≤ r ≤ 10,000) representing the number of cities in the network and number of roads,respectively. The following r lines will each describe one of the roads. Each of these lines will contain 3 positive integers u, v, p (1 ≤ u, v≤ c, u ≠ v, and 1 ≤ p ≤ 10,000) where u and v represent the two cities connected by the road and p represents the priority points of the road. It is possible that more than one road will connect the same pair of cities.
输出
For each input case, on a line by itself, output the total amount of priority points based on the rules the director has outlined.
样例输入
2
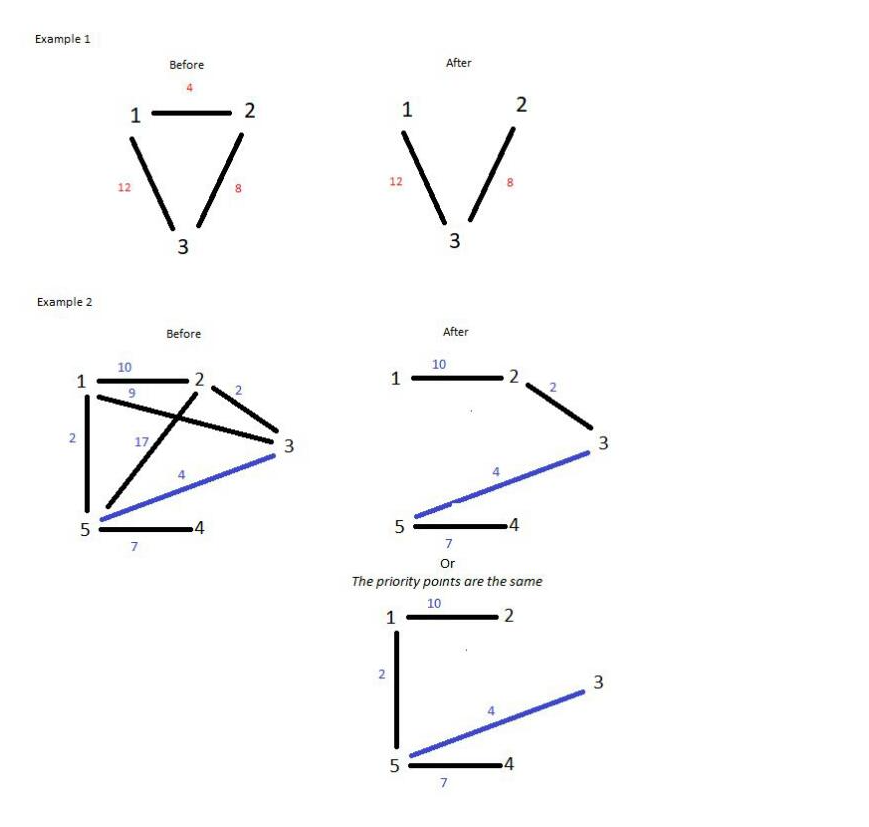
3 3
1 2 4
2 3 8
3 1 12
5 7
1 2 10
1 3 9
3 2 2
4 5 7
5 1 2
2 5 17
3 5 4
样例输出
20
23
提示
题目描述
给定一个图,对于其中的每个点,只留下一条出边,要求是:边权要尽量大,但是要优先选偶数边权的边,实际上就是按照题目要求找出最大生成树并输出边权之和。
思路
可以先将所有的边排序,排序规则按照题目描述即可,先按照奇偶性排序,再按照大小排序,然后用kruskal跑一边即可选出这棵特定的最大生成树。
代码
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 10010;
struct edge
{
int a, b, w;
bool operator< (const edge& r) const
{
if ((w & 1) != (r.w & 1)) return (r.w & 1) > (w & 1); // 按照奇偶排序
else return w > r.w; // 奇偶一样就按照大小排
}
}e[N];
int n, m;
int p[N];
void init()
{
for (int i = 1; i <= n; i ++ ) p[i] = i;
}
int find(int x)
{
if (x != p[x]) p[x] = find(p[x]);
return p[x];
}
int kru()
{
int ans = 0;
sort(e, e + m);
for (int i = 0; i < m; i ++ )
{
int a = e[i].a, b = e[i].b, w = e[i].w;
a = find(a), b = find(b);
if (a != b)
{
p[a] = b;
ans += w;
}
}
return ans;
}
int main()
{
int t;
cin >> t;
while (t -- )
{
cin >> n >> m;
init();
for (int i = 0; i < m; i ++ )
{
int a, b, w;
cin >> a >> b >> w;
e[i] = {a, b, w};
}
cout << kru() << endl;
}
return 0;
}
I.找路(Roads? Where We Are Going, We Don’t Need Roads.)
原文:https://www.cnblogs.com/lautoh/p/14641535.html