二叉树——543. 二叉树的直径

题目：

思路：

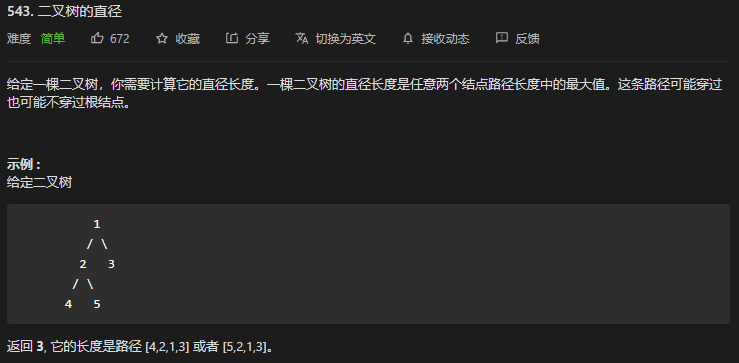
二叉树的直径，就是求最长路径然后减1。所以现在问题就变为了求最长路径的问题。

最长路径的问题又可以类比求最大路径和的问题，所以就是求左子树的最长路径和右子树的最长路径然后加上root结点就是最长路径了，遍历顺序自然和求最大路径和一样也是后序遍历，然后都有了，开始操作吧。

代码：

class Solution {
    int ans;
    int depth(TreeNode* node){
        // 访问到空节点了，返回0
        if(!node) return 0;
        int L = depth(node->left);     // 左 
        int R = depth(node->right);    // 右
        ans = max(ans, L+R+1);         // 中
        // 返回该节点为根的子树的深度
        return max(L,R) + 1;
    }
public:
    int diameterOfBinaryTree(TreeNode* root) {
        ans =1;
        depth(root);
        return ans - 1;
    }
};

Rank：

Tips：

就是虽然问法和求的东西不一样，但是本质是一样的，要类比，没准就有思路了。

二叉树——543. 二叉树的直径

原文：https://www.cnblogs.com/lzyrookie/p/14643375.html