64. 最小路径和

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例 1：

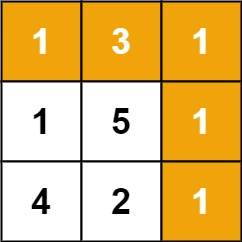
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

• 动态规划
  本题的dp数组含义比较容易确定，即\(dp[i][j]\)表示从起点到\((i,j)\)终点的最短距离。
• 更新公式类似，因为只能向下或者向右走，因此\(dp[i][j]\)由\(dp[i-1][j]\)和\(dp[i][j-1]\)中的较小值决定；
• 边界条件是第一行与第一列，特殊处理。
• 最后需要根据更新方程，检查一下如何遍历数组，\(dp[i-1][j]\)和\(dp[i][j-1]\)需要在\(dp[i][j]\)更新之前遍历过，因此有，\(i\)从前向后遍历是外层循环，\(j\)从前往后遍历是内层循环。

 int minPathSum(vector<vector<int>>& grid) {
        // 向下或向右行走
        // 动态规划
        // dp[i][j]: 表示从起点到dp[i][j]的最短路径
        
        int m = grid.size(), n = grid[0].size();
        vector<vector<int>> dp(m, vector<int>(n, 0));

        // 边界条件
        dp[0][0] = grid[0][0];
        for(int i = 1; i < m; ++i){
            dp[i][0] = dp[i-1][0] + grid[i][0];
        }
        for(int j = 1; j < n; ++j){
            dp[0][j] = dp[0][j-1] + grid[0][j];
        }

        // 更新方程
        for(int i = 1; i < m; ++i){
            for(int j = 1; j < n; ++j){
                dp[i][j] = min(dp[i-1][j]+grid[i][j], dp[i][j-1]+grid[i][j]);
            }
        }

        return dp[m-1][n-1];
    }

64. 最小路径和

原文：https://www.cnblogs.com/alyosha/p/14644704.html