单应性变换就是一个平面到另一个平面的映射关系。
图像中的2D点可以被表示成3D向量的形式，其中，。它被叫做点的齐次表达，位于投影平面上。所谓单应就是发生在投影平面上的点和线可逆的映射。其它叫法包括射影变换、投影变换和平面投影变换等。
单应变换矩阵是一个3*3的矩阵H。这个变换可以被任意乘上一个非零常数，而不改变变换本身。所以它虽然具有9个元素，但是具有8个自由度。这意味这它里面有8个未知参数待求。
典型地，可以通过图像之间的特征匹配来估计单应矩阵。
矩阵的一个重要作用是将空间中的点变换到另一个空间中。这个作用在国内的《线性代数》教学中基本没有介绍。要能形像地理解这一作用，比较直观的方法就是图像变换，图像变换的方法很多，单应性变换是其中一种方法，单应性变换会涉及到单应性矩阵。单应性变换的目标是通过给定的几个点（通常是4对点）来得到单应性矩阵。假设单应性矩阵为：
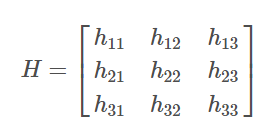
上面的矩阵$H$会将一幅图像上的一个点的坐标$a=(x,y,1)$映射成另一幅图像上的点的坐标$b=(x_1,y_1,1)$，但H是未知的。通常需要根据在同一平面上已知的一些点对(比如$a$,$b$)来求$H$。 假设已知点对($a$,$b$)，则有下面的公式：
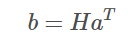
即：
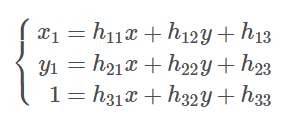
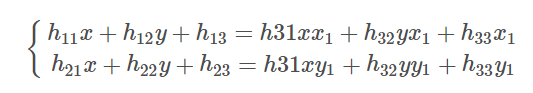
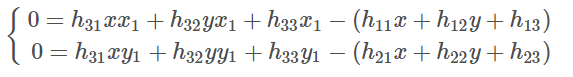
对于方程(1)可写成一个矩阵与一个向量相乘，即：
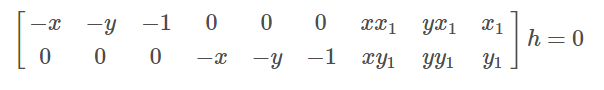
其中，$h=[h_{11} , h_{12} , h_{13} , h_{21} , h_{22} , h_{23} , h_{31} , h_{32} , h_{33}]^T$，是一个9维的列向量。若令: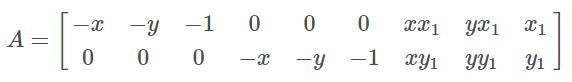
则$(???)(???)$可以记为
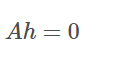这里的$A\in R^{2\times 9}$。这只是1对点所得到的矩阵$A$。究竟要多少点对才能求出$H$?由于我们是采用齐次坐标（即(x,y,1)）来表示平面上的点，所以存在一个非零的标量$s$，使得$b_1=sHa^T$与$b=sHa^T$都表示同一个点$b$。若令$s=\frac{1}{h_{33}}$，则$\frac{1}{h_{33}}H$为
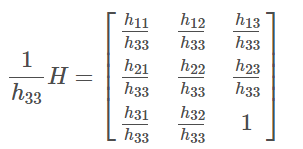
从公式$(???)(???)$可以看出，其实$H$只有8个变量（8个自由度）。因此，只需要4个点对，然后通过解线性方程组就可以求得$H$。也可以多于4个点对。
假设有$n\geq 4$个点对，则得到的矩阵$A\in R^{2n\times 9}$。如何求解向量$h$呢？方法很简单，真接对$A$进行SVD分解，即
然后取$V$的最后一列出来作为求解$h$。因为矩阵$A$是行满秩，即只有一个自由度。
具体实现时，先要得到两幅图，然后在两幅图之间找到4对点的坐标，由此得到矩阵$A$，然后在matlab中可以这样实现:
[U,S,V]=svd(A);
h=V(:,9);
H= reshape(h,3,3);
由单应性矩阵可以得到仿射变换，还可以在单应性矩阵上做图像拼接。
单应性矩阵可以有两幅图像（或者平面）中对应点对计算出来。前面已经提到过，一个完全射影变换具有8个自由度。根据对应点约束，每个对应点对可以写出两个方程，分别对应于x和y坐标。因此，计算单应性矩阵H需要4个对应点对。
DLT（Direct Linear Transformation，直接线性变换）是给定4个点或者更多对应点对矩阵，来计算单应性矩阵H的算法。将单应性矩阵H作用在对应点上，重新写出该方程，我们可以得到下面的方程：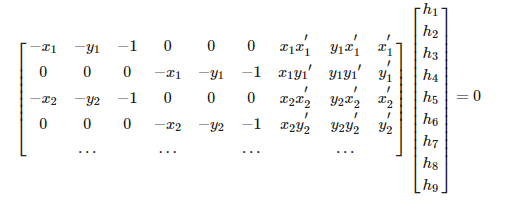
def H_from_points(fp, tp):
"""使用线性DLT方法，计算单应性矩阵H，使fp映射到tp。点自动进行归一化"""
if fp.shape != tp.shape:
raise RuntimeError(‘number of points do not match‘)
# 对点进行归一化（对数值计算很重要）
# --- 映射起始点 ---
m = mean(fp[:2], axis=1)
maxstd = max(std(fp[:2], axis=1)) + 1e-9
C1 = diag([1/maxstd, 1/maxstd, 1])
C1[0][2] = -m[0]/maxstd
C1[1][2] = -m[1]/maxstd
fp = dot(C1,fp)
# --- 映射对应点 ---
m = mean(tp[:2], axis=1)
maxstd = max(std(tp[:2], axis=1)) + 1e-9
C2 = diag([1 / maxstd, 1 / maxstd, 1])
C2[0][2] = -m[0] / maxstd
C2[1][2] = -m[1] / maxstd
tp = dot(C2, tp)
# 创建用于线性方法的矩阵，对于每个对应对，在矩阵中会出现两行数值
nbr_correspondences = fp.shape[1]
A = zeros((2 * nbr_correspondences, 9))
for i in range(nbr_correspondences):
A[2*i] = [-fp[0][i], -fp[1][i],-1,0,0,0,
tp[0][