221. 最大正方形

在一个由 ‘0‘ 和 ‘1‘ 组成的二维矩阵内，找到只包含 ‘1‘ 的最大正方形，并返回其面积。

示例 1：

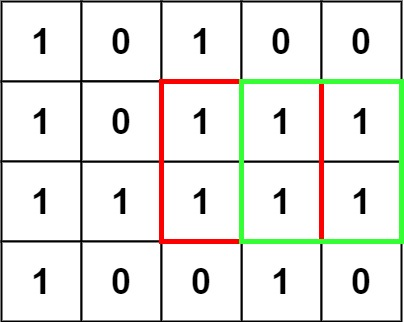
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：4

动态规划

• 本题需要仔细考虑的是dp数组代表的含义。
• 首先题目中寻找的是正方形，因此我们可以寻找正方形的边长即可。
• 二维dp数组，\(dp[i][j]\)代表以\((i,j)\)为右下角的最大正方形边长。（稍微有点难想到。。）
• 更新方程：若当前\(matrix[i][j] == ‘1‘\)，判断可否延长该正方形，这根据上方，左上，左方的最短边长决定，i.e.,
• \(min(dp[i-1][j], dp[i-1][j-1], dp[i][j-1])\)
• 最后注意边界条件，第一行与第一列。然后寻找dp数组中的最大元素及对应最大边长。

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        // 正方形，因此寻找边长即可
        // dp[i][j], 表示以i,j为右下角的正方形边长。
        // dp[i-1][j], dp[i-1][j-1], dp[i][j-1]中最短的边长， 再加上matrix[i][j]
        int m = matrix.size(), n = matrix[0].size(), ans = 0;
        vector<vector<int>> dp(m, vector<int>(n,0));
        for(int i = 0; i < m; ++i){
            for(int j = 0; j < n; ++j){
                // 边界条件
                if(!i)
                    dp[0][j] = (matrix[0][j] == ‘1‘); 
                else if(!j)
                    dp[i][0] = (matrix[i][0] == ‘1‘);
                // 更新方程
                else if( matrix[i][j] == ‘1‘){
                    int tmp = min(dp[i-1][j], dp[i][j-1]);
                    dp[i][j] = min(tmp, dp[i-1][j-1]) + 1;    
                }
                ans = max(ans, dp[i][j]);
            }
        }
        return ans*ans;
    }
};

221. 最大正方形

原文：https://www.cnblogs.com/alyosha/p/14646301.html