DP 矩阵连乘问题
动态规划:
矩阵链乘法问题可表述如下:给定n个矩阵构成的一个链<A1,A2,A3……An>,其中i=1,2,……n,矩阵Ai维数为P.i-1×P.i,对乘积A1·A2·A3···An以最小化标量乘法次数的方式进行加括号。
注:矩阵链问题主要涉及的时在多个矩阵相乘,如何通过相乘的顺序来减少程序运行。
递推规律:
设计算A[i:j](矩阵A从i乘到j),1≤i≤j≤n,所需要的最少数乘次数m[i,j],则原问题的最优值为m[1,n](上面例题就是m[1][6])。
当i=j时,A[i:j]=Ai,因此,m[i][i]=0,i=1,2,…,n 当i<j时,若A[i:j]的最优次序在Ak和Ak+1之间断开,i<=k<j,则:m[i][j]=m[i][k]+m[k+1][j]+pi-1pkpj。由于在计算是并不知道断开点k的位置,所以k还未定。不过k的位置只有j-i个可能。因此,k是这j-i个位置使计算量达到最小的那个位置。
综上,有递推关系如下:
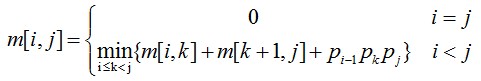


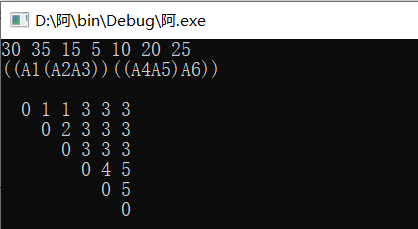
测试 :A1 {30*35} A2{35*15} A3{15*5} A4{5*10} A5{10*20} A6{20*25}
#include <iostream> #include<vector> using namespace std; const int n=6; void trace(int i,int j,int s[][n+1]) { if(i==j) { cout<<‘A‘<<i; } else{ cout<<‘(‘; int k; k=s[i][j]; trace(i,k,s); trace(k+1,j,s); cout<<‘)‘; } } int main() { //cin>>n; //n个矩阵 int maj[n+1]; //一维数组储存n个矩阵的维数 A1,A2,A3……An int k; int fz[n+1][n+1]; int point[n+1][n+1]; // 记录最小间断位置 只用1-n 空0号 for(k=0;k<n+1;k++) { cin>>maj[k]; fz[k][k]=0;//对角线元素赋0 自己相乘为0 point[k][k]=0; } int i,r,j; for(r=2;r<=n;r++) //r用来确定 行i与列j之间的关系 for(i=1;i<=n-r+1;i++) { j=r+i-1; fz[i][j]=fz[i+1][j]+maj[i-1]*maj[i]*maj[j]; // 先把第一个,与后面分开 point[i][j]=i; for(k=i+1;k<j;k++) //间断位置 { int minsum=fz[i][k]+fz[k+1][j]+maj[i-1]*maj[k]*maj[j]; if(minsum<fz[i][j]) { fz[i][j]=minsum; point[i][j]=k; //将间断位置存给point } } } trace(1,6,point); //输出 cout<<"\n\n"; for(i=1;i<=n;i++) {int m; for(m=1;m<=i;m++) cout<<" "; for(j=i;j<=n;j++) {cout<<point[i][j]<<‘ ‘; if(j==n) cout<<‘\n‘;}} }
原文:https://www.cnblogs.com/ljh354114513/p/14650240.html