插值 Interpolation

1. Linear interpolation

|----|----------------|
x0   x               x1

     ( x - x0 )
t = ------------ 
     ( x1 - x0 )
t 就是到小端的距离占总距离的比例

x = x0 + t * ( x1 - x0 )

x = ( 1 - t ) * x0 + t * x1
t 越大，说明到小端的距离占总距离的比例越大，i.e. 越靠近大端

e.g.
x0 = 0, x1 = 10, x = 2
t = ( 2 - 0 ) / ( 10 - 0 ) = 0.2
x = ( 1 - 0.2 ) * 0 + 0.2 * 10 = 0.8 * 0 + 0.2 * 10 = 2

也就是说，比例越大，大端的成分越多，所以大端系数越大

【非常不严谨地说】 t 虽然是用“小端算出来”的，但是它跟“大端是一伙”的

2. Bilinear interpolation

+-----+---+----+-----+ y1
|     |   |    |     |
+-----+---+----+-----+ y
|     |   |    |     |
+-----+---+----+-----+ y0
|     |   |    |     |
+-----+---+----+-----+
      x0  x    x1
      
x = ( 1 - u ) * x0 + u * x1
y = ( 1 - v ) * y0 + v * y1

给定的是四个点 (x0, y0), (x0, y1), (x1, y0), (x1, y1)。
所谓 Bilinear 指的是在两个方向上做 Linear，但是线性插值的次数有 3 次。
注意线性插值只能在两者之间插值，所以第一次用 4 个点插值出来 2 个点，第二次用这 2 个点插值出来 1 个点。

【1】 x 方向插值

(x, y0) = ( 1 - u ) * (x0, y0) + u * (x1, y0)
(x, y1) = ( 1 - u ) * (x0, y1) + u * (x1, y1)

【2】 y 方向插值

(x, y) = ( 1 - v ) * (x, y0) + v * (x, y1)

3. 给点指定上函数值

Linear interpolation

f(x) = ( 1 - t ) * f(x0) + t * f(x1)

如果不给出系数 t ，给出 x 的话，由于

     ( x - x0 )
t = ------------ 
     ( x1 - x0 )

就变成

       ( x1 - x )            ( x - x0 )
f(x) = ----------- * f(x0) + ----------- * f(x1)
       ( x1 - x0 )           ( x1 - x0 )

Bilinear interpolation

【1】 x 方向插值

f(x, y0) = ( 1 - u ) * f(x0, y0) + u * f(x1, y0)
f(x, y1) = ( 1 - u ) * f(x0, y1) + u * f(x1, y1)

【2】 y 方向插值

f(x, y) = ( 1 - v ) * f(x, y0) + v * f(x, y1)

如果不给出系数 u 和 v ，给出 x 和 y 的话，由于

     ( x - x0 )
u = ------------ 
     ( x1 - x0 ) 

     ( y - y0 )
v = ------------ 
     ( y1 - y0 ) 

就变成

【1】 x 方向插值

           ( x1 - x )                ( x - x0 )
f(x, y0) = ----------- * f(x0, y0) + ----------- * f(x1, y0)
           ( x1 - x0 )               ( x1 - x0 )                             

           ( x1 - x )                ( x - x0 )
f(x, y1) = ----------- * f(x0, y1) + ----------- * f(x1, y1)
           ( x1 - x0 )               ( x1 - x0 )                             

【2】 y 方向插值

          ( y1 - y )               ( y - y0 )
f(x, y) = ----------- * f(x, y0) + ----------- * f(x, y1)
          ( y1 - y0 )              ( y1 - y0 )                             

4. Trilinear interpolation

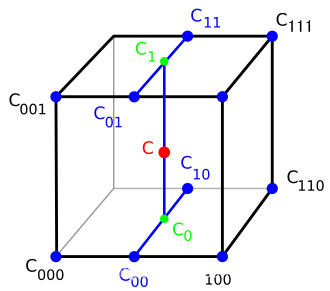
同理不再赘述：有三个参数 u, v, w ，需要给出 8 个点（ 8 => 4 => 2 => 1 ）。

插值 Interpolation

原文：https://www.cnblogs.com/tandandan/p/14659751.html