什么是单源最短路径?
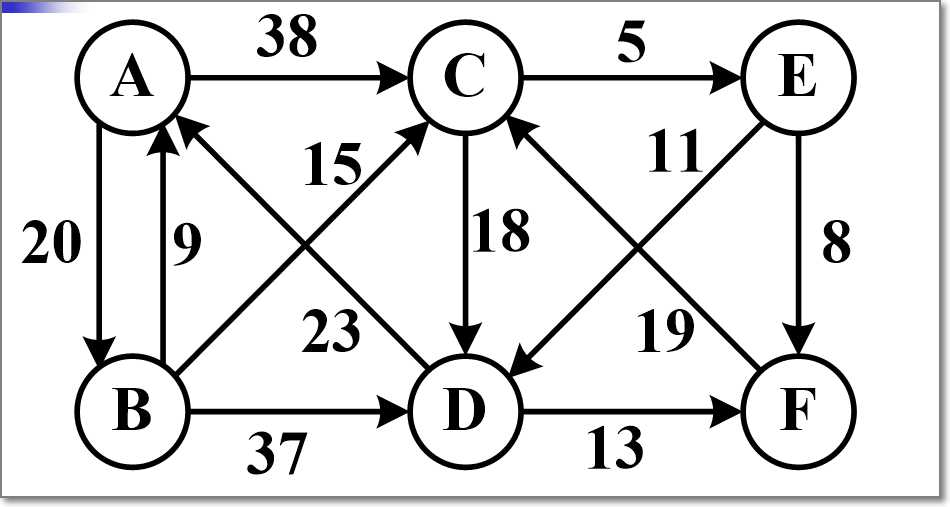
现在有6个结点,只求A到B、C、D、E、F的最短路径,而不同时求B到其他结点,C到其他结点,D到其他结点,E到其他结点,F到其他结点的最短路径。即只求某一个结点到其他结点的最短路径。
Dijkstra算法是什么意思?
现在试求A到B、C、D、E、F的最短路径。
先准备一个集合S,里面存放已经找到最短路径的结点,A到A一定是最短路径,故先把A放入集合S,即集合S:{A}
从A出发找相邻的,到B、C的距离是20、38,选最小的,将B放入集合S,即集合S:{A,B}。A→B的最短路径经过A、B
从B出发找相邻的,到A、C、D的距离是9、15、37,到A的已经在集合S中了,忽略;到C一共是35,到D一共是57。发现35比38小,集合S:{A,B,C}。A→C的最短路径经过A、B、C
从C出发找相邻的,到D、E的距离是18、5,到D一共的距离是53,到E一共的距离是40,53小于57,集合S:{A,B,C,D}。A→D的最短路径经过A、B、C、D
从D出发找相邻的,到A、F的距离是23、13,到A的忽略,到F一共的距离是66,没有到E的,那上面到E的就是最短路径,集合S:{A,B,C,D,E}。A→E的最短路径经过A、B、C、E
从E出发找相邻的,到D、F的距离是11、8,到D的忽略,到F一共的距离是48,48小于66,集合S:{A,B,C,D,E,F}。A→F的最短路径经过A、B、C、E、F
和Prim算法一样一样的!还是有区别的
最小生成树所有结点都是相连的,单源最短路径不必所有结点都相连,只要源点与所有结点都相连就可以
单源最短路径的Dijkstra算法和多源最短路径的Floyd算法
原文:https://www.cnblogs.com/jinlin-2018/p/14661913.html