最短路径(dijkstra算法, C语言)

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
/*
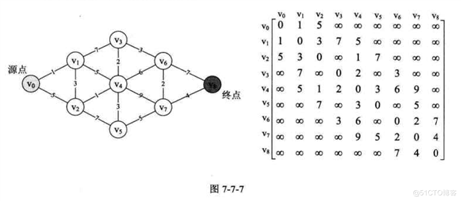
 * 代码实现<<大话数据结构>>p262 图7-7-7,v0至v8分别用ABCDEFGHI代替
 * 执行完此算法可以通过2个数组得到源点到任意1个终点的最短路径及开销
 */

#define MAX 9
#define INFINITY 65535
typedef int PreNode[MAX]; // 存放最短路径中各节点的上一个节点
typedef int PathMatrix[MAX]; // 存放源点到各节点的最短路径开销

// 图结构体
typedef struct {
    char vexs[MAX]; // 顶点的数组，顶点类型为了简单使用char
    int arc[MAX][MAX]; // 边表二维数组，值为权
    int numVex;
}GRAPH, *PGRAPH;

void create(PGRAPH);
void gprint(GRAPH);
void addEdge(PGRAPH, int, int, int);
void dijkstra(GRAPH, int, PreNode *, PathMatrix *);

// 求start到所有顶点的最短路径及开销，结果保存在P和M数组中
// start这里以0举例，下面的start节点都表示0节点
void dijkstra(GRAPH graph, int start, PreNode *P, PathMatrix *M)
{
    int v, w, k, min;

    int final[MAX]; // 标识已经确认最短路径的顶点，为1表示已经确认
    // 先用start节点及相关的边进行初始化操作
    for (v=0; v<graph.numVex; v++) {
        (*M)[v] = graph.arc[start][v]; //与start有关的边的权值初始化到D数组
        final[v] = 0; // 所有顶点初始化为未确认状态
        (*P)[v] = -1; // 所有顶点的前一个节点标识为未确认状态
    }
    // 对start节点的特殊初始化
    (*M)[start] = 0; // start到自身的权值为0，这一步感觉多余
    final[start] = 1; // start到自身标识为已确认最短路径

    // 正式开始循环处理，每次循环都能找到最短路径的下一个顶点
    // 根据M数组查找最小权值顶点（也就是最短路径中下一个顶点）
    for (v=1; v<graph.numVex; v++) {
        min = INFINITY;
        for (w=0; w<graph.numVex; w++) {
            if (!final[w] && (*M)[w] < min) {
                min = (*M)[w]; // 更新min
                k = w; // 保存最小值
            }
        }

        final[k] = 1; // k为新确认的最短路径中的节点

        // 把比对k相关的边的权值更新到数组（根据k会新发现与其有关的顶点）
        for (w=0; w<graph.numVex; w++) {
            /* 对于首次发现的顶点为65535肯定要更新
             * 对于非首次发现的顶点如果从最短路径经过到此节点比原来的权和小，则
             *   说明找到了新的最短路径，更新M权值数组，及P关系节点数组
             */
            if (!final[w] && min + graph.arc[k][w] < (*M)[w]) {
                (*M)[w] = min + graph.arc[k][w];
                (*P)[w] = k;
            }
        }
    }
}

void addEdge(PGRAPH g, int i, int j, int v)
{
    g->arc[i][j] = g->arc[j][i] = v;
}

void create(PGRAPH g)
{
    int i, j;

    g->numVex = 9;
    // 创建顶点
    g->vexs[0] = ‘A‘;
    g->vexs[1] = ‘B‘;
    g->vexs[2] = ‘C‘;
    g->vexs[3] = ‘D‘;
    g->vexs[4] = ‘E‘;
    g->vexs[5] = ‘F‘;
    g->vexs[6] = ‘G‘;
    g->vexs[7] = ‘H‘;
    g->vexs[8] = ‘I‘;
    // 初始化边表矩阵
    for (i=0; i<g->numVex; i++) {
        for (j=0; j<g->numVex; j++) {
            g->arc[i][j] = INFINITY;
            if (j == i)
                g->arc[i][j] = 0; //行列相等时表示自身，标识为0
        }
    }
    // 添加边及权值
    // A v0, B v1, C v2, D v3, E v4, F v5, G v6, H v7, I, v8
    addEdge(g, 0, 1, 1);
    addEdge(g, 0, 2, 5);
    addEdge(g, 1, 2, 3);
    addEdge(g, 1, 4, 5);
    addEdge(g, 1, 3, 7);
    addEdge(g, 2, 4, 1);
    addEdge(g, 2, 5, 7);
    addEdge(g, 3, 4, 2);
    addEdge(g, 3, 6, 3);
    addEdge(g, 4, 5, 3);
    addEdge(g, 4, 7, 9);
    addEdge(g, 4, 6, 6);
    addEdge(g, 5, 7, 5);
    addEdge(g, 6, 7, 2);
    addEdge(g, 6, 8, 7);
    addEdge(g, 7, 8, 4);
}

void gprint(GRAPH graph)
{
    int i, j;
    for (i=0; i<graph.numVex; i++) {
        for (j=0; j<graph.numVex; j++){
            printf("%6d ", graph.arc[i][j]);
        }
        putchar(‘\n‘);
    }

}

int main(void)
{
    GRAPH graph;
    PreNode pre_node;
    PathMatrix path_matrix;
    int i;

    create(&graph);
    gprint(graph);
    dijkstra(graph, 0, &pre_node, &path_matrix);
    printf("v0到各顶点的最短路径(-1表示前顶点为start):\n");
    for (i=0; i<MAX; i++) {
        printf("%d ", pre_node[i]);
    }
    putchar(‘\n‘);

    printf("v0到各顶点的最短路径权值和:\n");
    for (i=0; i<MAX; i++) {
        printf("%d ", path_matrix[i]);
    }
    putchar(‘\n‘);

    return 0;
}

output

[root@8be225462e66 c]# ./a.out
     0      1      5  65535  65535  65535  65535  65535  65535
     1      0      3      7      5  65535  65535  65535  65535
     5      3      0  65535      1      7  65535  65535  65535
 65535      7  65535      0      2  65535      3  65535  65535
 65535      5      1      2      0      3      6      9  65535
 65535  65535      7  65535      3      0  65535      5  65535
 65535  65535  65535      3      6  65535      0      2      7
 65535  65535  65535  65535      9      5      2      0      4
 65535  65535  65535  65535  65535  65535      7      4      0
v0到各顶点的最短路径(-1表示前顶点为start):
-1 -1 1 4 2 4 3 6 7
v0到各顶点的最短路径权值和:
0 1 4 7 5 8 10 12 16
[root@8be225462e66 c]#

最短路径(dijkstra算法, C语言)

原文：https://blog.51cto.com/sndapk/2711320