DP-覆盖墙壁

你有一个长为N宽为2的墙壁，给你两种砖头：一个长2宽1，另一个是L型覆盖3个单元的砖头。如下图：

0  0
0  00

砖头可以旋转，两种砖头可以无限制提供。你的任务是计算用这两种来覆盖N*2的墙壁的覆盖方法。例如一个2*3的墙可以有5种覆盖方法，如下：

012 002 011 001 011  
012 112 022 011 001

注意可以使用两种砖头混合起来覆盖，如2*4的墙可以这样覆盖：

0112
0012

给定N，要求计算2*N的墙壁的覆盖方法。由于结果很大，所以只要求输出最后4位。例如2*13的覆盖方法为13465,只需输出3465即可。如果答案少于4位，就直接输出就可以，不用加0，如N=3，时输出5。

一个整数N（1<=N<=1000000），表示墙壁的长。

输出覆盖方法的最后4位，如果不足4位就输出整个答案。

思路：

　　最开始的思路是自底向上，观察N与N-1的结果计算有没有什么关联，掉入了思维惯性，看了半天没有发现N的结果怎么从前面的得来。

　　之后转变了思路，该题的突破点在于分析墙的尾部。

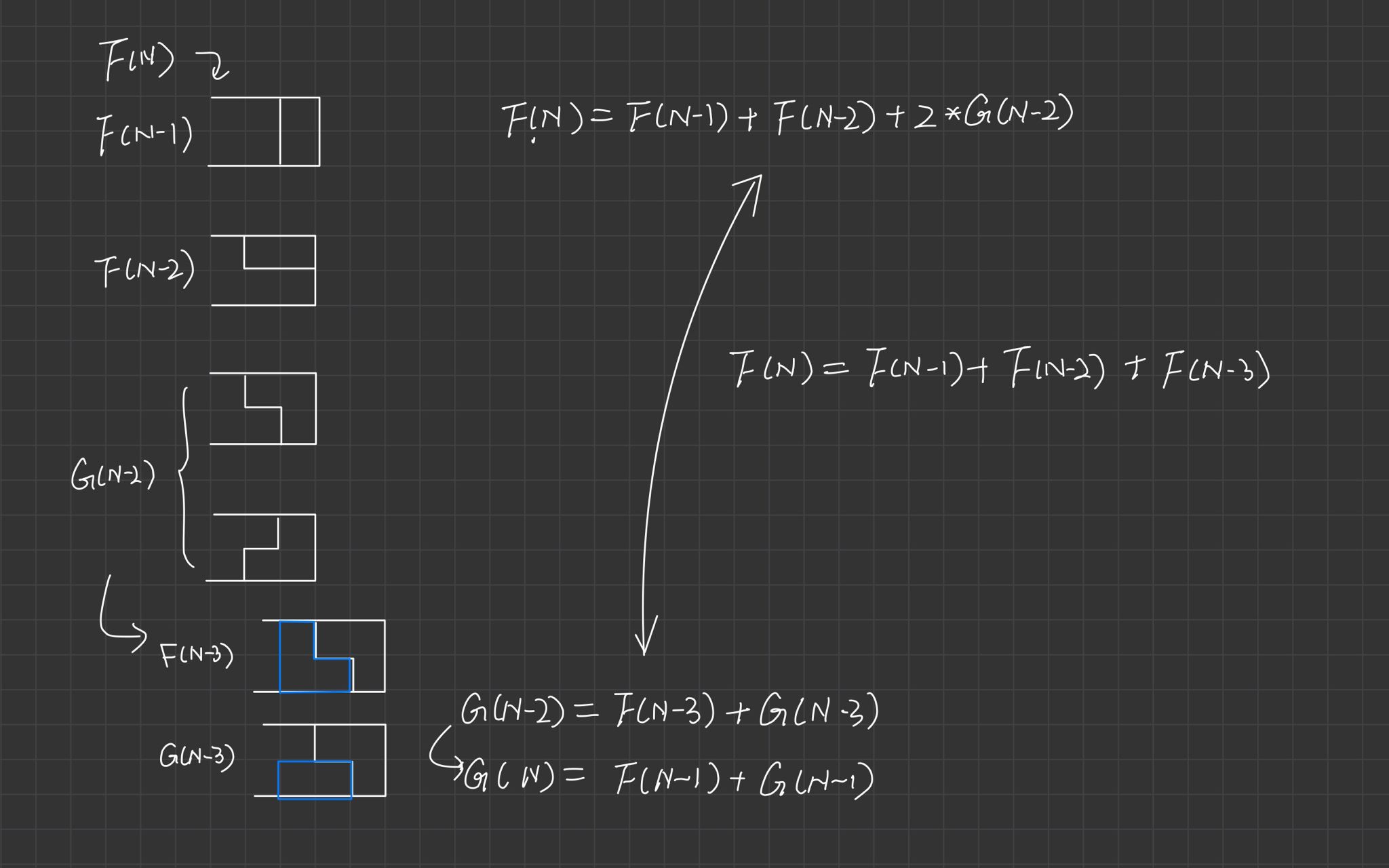
初始值F[0]=F[1]=G[1]=1,G[0]=0。其中F[1]和G[1]可以直接算出来，F[0]和G[0]是结合递推公式得到的。

代码

#include <iostream>
using namespace std;
#define mod 10000
const int maxn = 1000100;
int F[maxn],G[maxn];
int main() {
    int N;
    while (cin >> N) {
        F[0] = 1;
        F[1] = 1;
        G[0] = 0;
        G[1] = 1;
        for (int i = 2; i <= N; i++) {
            F[i] = (F[i - 1] + F[i - 2] + 2 * G[i - 2]) % mod;
            G[i] = (G[i - 1] + F[i - 1]) % mod;
        }
        cout << F[N] << endl;
    }
}