回溯算法三：经典问题实现示例

问题分析过程，可以参考：回溯算法一：算法介绍与经典问题分析
算法框架分析过程，可以参考：回溯算法二：算法框架与实现

一、m-着色问题

根据问题分析以及回溯框架简化，代码实现如下：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

int isPartial(int *G, int n, int *x, int k)
{
    for (int i = 0; i < k; i++) {
        // 根据邻接表判断两个节点之间是否相邻，再进一步判断其配色是否相同,x中按顺序保存各节点的配色
        if ((G[i * n + k] == 1) && (x[i] == x[k])) {
            return 0;
        }
    }
    return 1;
}

// 递归过程，x与k同时变化，其他均为定值
void generalExplore(int *G, int n, int *colors, int m, int *x, int k)
{
    int i;
    // 完全解判断：k为当前解长度，n为完整解的最大长度
    if (k >= n) {
        for (int i = 0; i < n; i++) {
            printf("%d ", x[i]);
        }
        printf("\n");
        return;
    }
    // 无解退出
    if (k >= n) {
        return;
    }
    // 递归遍历，回溯过程
    for (int i = 0; i < m; i++) {
        // 当前节点的取值集合，根据问题分析，通常可以确定
        x[k] = colors[i];
        // 判断部分解逻辑复杂，建议抽取函数
        if (isPartial(G, n, x, k)) {
            generalExplore(G, n, colors, m, x, k + 1);
        }
    }
}

int main(void)
{
    // G为邻接矩阵，n为解向量长度，color为颜色集合，m为颜色种类，x为解向量空间，k为当前解的个数[0, n-1]
    int n = 5;
    int G[25] = {0, 1, 1, 0, 0,
                 1, 0, 0, 1, 1,
                 1, 0, 0, 1, 1,
                 0, 1, 1, 0, 1,
                 0, 1, 1, 1, 0};
    int m = 3;
    int colors[] = {1, 2, 3};
    int *x = (int*)calloc(n, sizeof(int));
    int k = 0;

    generalExplore(G, n, colors, m, x, k);
    while(1);
    return 0;
}

测试结果：

二、 n-皇后问题

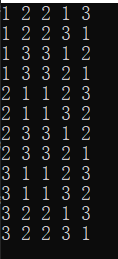
该代码实现与着色问题仅修改了部分解判断条件和函数入参，可见框架适应性较强：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

int isPartial(int n, int *x, int k)
{
    int diff;
    for (int i = 0; i < k; i++) {
        // 判断新增的位置与历史位置是否满足规则：不同行、不同列、不同斜线
        diff = x[i] - x[k];
        if (diff == 0 || (diff == i - k) || (diff == k - i)) {
            return 0;
        }
    }
    return 1;
}

// 递归过程，x与k同时变化，其他均为定值
void nQueens(int n, int *locations, int *x, int k)
{
    int i;
    // 完全解判断：k为当前解长度，n为完整解的最大长度
    if (k >= n) {
        for (int i = 0; i < n; i++) {
            printf("%d ", x[i]);
        }
        printf("\n");
        return;
    }
    // 无解退出
    if (k >= n) {
        return;
    }
    // 递归遍历，回溯过程
    for (int i = 0; i < n; i++) {
        // 当前节点的取值集合，根据问题分析，通常可以确定
        x[k] = locations[i];
        // 判断部分解逻辑复杂，建议抽取函数
        if (isPartial(n, x, k)) {
            nQueens(n, locations, x, k + 1);
        }
    }
}

int main(void)
{
    // n为棋盘规模，x为解向量空间，k为当前解的个数[0, n-1]
    int n = 4;
    int k = 0;
    // x[i]表示第i行上，皇后对应的列的位置
    int *x = (int*)calloc(n, sizeof(int));
    int locations[] = {0, 1, 2, 3, 4};
    
    // n为棋盘规模，locations为棋盘位置集合（列），x为解向量空间，k为当前解的个数[0, n-1]
    nQueens(n, locations, x, k);
    while(1);
    return 0;
}

测试结果：

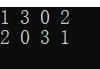
结果表明，4皇后有两种方案，[1, 3, 0, 2]表示每行的列的序号，实际摆放如下：

三、Hamilton回路

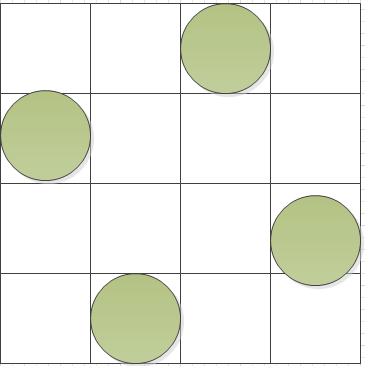
代码实现：

待处理

测试代码：

四、子集和

代码实现：

待处理

测试代码：

回溯算法三：经典问题实现示例

原文：https://www.cnblogs.com/HZL2017/p/14669310.html