均匀随机数生成

??先来说说均匀随机数生成，这是非均匀随机数的生成基础。

??例如，我们现在有drand()函数，可以随机生成[0,1]范围内的均匀随机数.

要求一个drand2()函数，能够生成[0,2]内的均匀随机数。

??显然有：

??但是很多时候，我们希望生成的随机数是有一定概率偏向的。

??比如生成[0,2]的随机数，越偏向2的数，出现的概率越大，显然上面的\(2*drand()\)无法满足要求。

??我们的随机数的概率密度分布如下：

生成指定概率密度的随机数

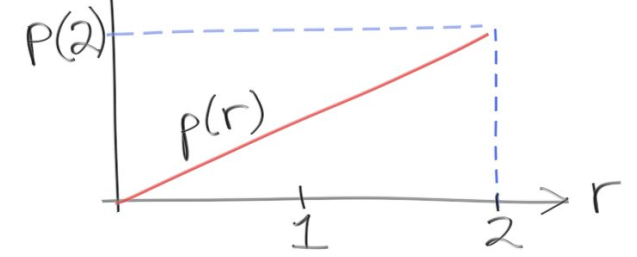
??先上结论：

??设概率密度函数\(f(x)\)，概率累计分布函数\(F(x)\)

??生成概率密度为p(x)的随机数的函数如下：

证明

??设概率密度函数\(f(x)\)，概率累计分布函数\(F(x)\)，\(\xi\)表示服从\((0,1)\)均匀分布的随机变量，变换函数为\(G\)，随机变量\(X=G(\xi)\)，其中\(F(x)\)为单调递增函数。

??由概率分布定义知：

??若\(G(\xi)\)为单调递增函数，可得：

??已知\(\xi\)在\((0,1)\)上均匀分布，可得：

??故有F,G互为反函数，即：

更多拓展见：https://zhuanlan.zhihu.com/p/191487550

蒙特卡洛——使用CDF反函数生成非均匀随机数

原文：https://www.cnblogs.com/mingyangovo/p/14668731.html