给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
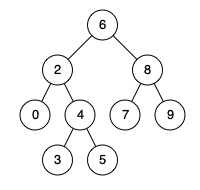
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
1.解题思路
方法一:先找出所求两个结点的路径,再对它们的路径一一比较,看看是从哪里分开的
class Solution: def lowestCommonAncestor(self, root: ‘TreeNode‘, p: ‘TreeNode‘, q: ‘TreeNode‘) -> ‘TreeNode‘: def _get_path(root, node): stack = [] cur = root while cur != node: stack.append(cur) if node.val > cur.val:cur = cur.right else:cur = cur.left stack.append(cur) return stack p_path = _get_path(root, p) q_path = _get_path(root, q) res = [] i = 0 while p_path[i] == q_path[i]: res.append(p_path[i]) i += 1 if i >= min(len(p_path), len(q_path)):break return res[-1]
方法二:注意到题目条件是搜索二叉树,那也就是说对于某个结点来说,其左孩子的值小于它的值,而其右孩子的值大于它的值。
如果当前结点的值比这两个结点的值都要大,那说明这两个结点都在其左子树上,反之就在其右子树上。
如果当前结点的值处于两个结点的值之间,就说明该节点是它们的分岔点。
若在寻找路径的过程中碰到了其中之一,就没有往下继续搜索的必要了,这个结点就是另一个结点的最近祖先结点。
class Solution: def lowestCommonAncestor(self, root: ‘TreeNode‘, p: ‘TreeNode‘, q: ‘TreeNode‘) -> ‘TreeNode‘: cur = root max_val = max(p.val, q.val) min_val = min(p.val, q.val) while cur: if cur.val < min_val:cur = cur.right if cur.val > max_val:cur = cur.left if cur.val > min_val and cur.val < max_val: return cur if cur.val == p.val or cur.val == q.val: return cur
原文:https://www.cnblogs.com/Souriez/p/14669035.html