设 \(A\) 是一个 \(n\times m\) 的矩阵,\(B\) 是一个 \(m\times p\) 的矩阵,那么 \(A\times B\) 的结果 \(C\) 中的元素为:
运算过程就是下面这样:
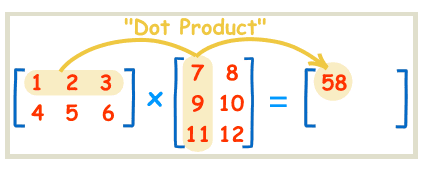
由于矩阵满足结合律和分配律,所以可以使用快速幂。
一个经典的例子是 \(\mathcal O(\log n)\) 的时间复杂度求斐波那契数列的第 \(n\) 项。假设第 \(i\) 项为 \(f_i\),那么有:
答案就是求 \(\left[\begin{matrix}f_{0} & f_{1}\end{matrix}\right]\times\left[\begin{matrix}0 & 1\\1 & 1\end{matrix}\right]^{n-1}=\left[\begin{matrix}0 & 1\end{matrix}\right]\times\left[\begin{matrix}0 & 1\\1 & 1\end{matrix}\right]^{n-1}\) 第 \(1\) 行第 \(2\) 列的数,对 \(\left[\begin{matrix}0 & 1\\1 & 1\end{matrix}\right]^{n-1}\) 快速幂求解即可做到 \(\mathcal O(\log n)\)。
原文:https://www.cnblogs.com/juruo-zzt/p/14670467.html