顺序表的应用-有序表合并问题

设计一个函数，将两个顺序存储的严格递增的有序表合并成一个严格递增的有序表。

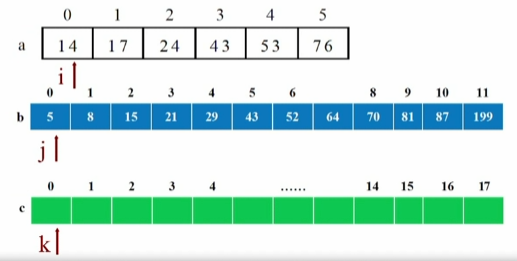
如上图所示

设置三个指针 i，j，k，

i指向a[0]，

比较 a[i] 和 和 b[j] 的值。

设置指针 i 让其指向 a[0]；

设置指针 j 让其指向 b[0]；

设置指针 k让其指向 c[0]；

比较 a[i] 和 b[j] 的值（此刻是 a[0] 和 b[0] 的值）

∵ a[0] = 14，b[0] = 5    ∴ 将 5 复制到 c[0] 位置。k 右移一位，i 不动，j 右移一位；

比较 a[i] 和 b[j] 的值（此刻是 a[0] 和 b[1] 的值）

∵ a[0] = 14，b[1] = 8    ∴ 将 8 复制到 c[1] 位置。k 右移一位，i 不动，j 右移一位；

比较 a[i] 和 b[j] 的值（此刻是 a[0] 和 b[2] 的值）

∵ a[0] = 14，b[2] = 15    ∴ 将 14 复制到 c[2] 位置。k 右移一位，i 右移一位，j 不动；

 反复如此，直到有一个数组首先被看完，将算法思想形式化，就得到如下函数：

int merge(int a[], int m, int b[], int n, int c[]){
    // 传入参数 m，n 分别是数组 a 和 b 的长度
    int i=0; j=0; k=0;
    while( i<m && j<n ){
        // 数组a元素小于数组b对应元素时，将数组a此元素放入数组c中
        if(a[i]<b[j]){
            c[k++] = a[i++];
        // 数组b元素小于数组a对应元素时，将数组b此元素放入数组c中
        }else if(b[j]<a[i]){
            c[k++] = b[j];
        }else{
            c[k++] = b[j++];
            i++;
        }
        while(j<m){
            c[k++] = a[i++]; // 复制剩余数据段
        }
        while(j<n){
            c[k++] = b[j++]; // 复制剩余数据段
        }
        return k; // 返回值 k 是数组 c 的长度
    }
}

我们不妨换种角度去理解：对于数组C而言，数组a 和 数组b 就是数据源。

我们按照规则完成了对 数组C 的构造工作，每次都是在表尾插入一个新的元素。

对 数组a 和 数组b 的访问流程，本质上就是顺序查找。

顺序表的应用-有序表合并问题

原文：https://www.cnblogs.com/AronKeener/p/14671975.html