放一个精选题解
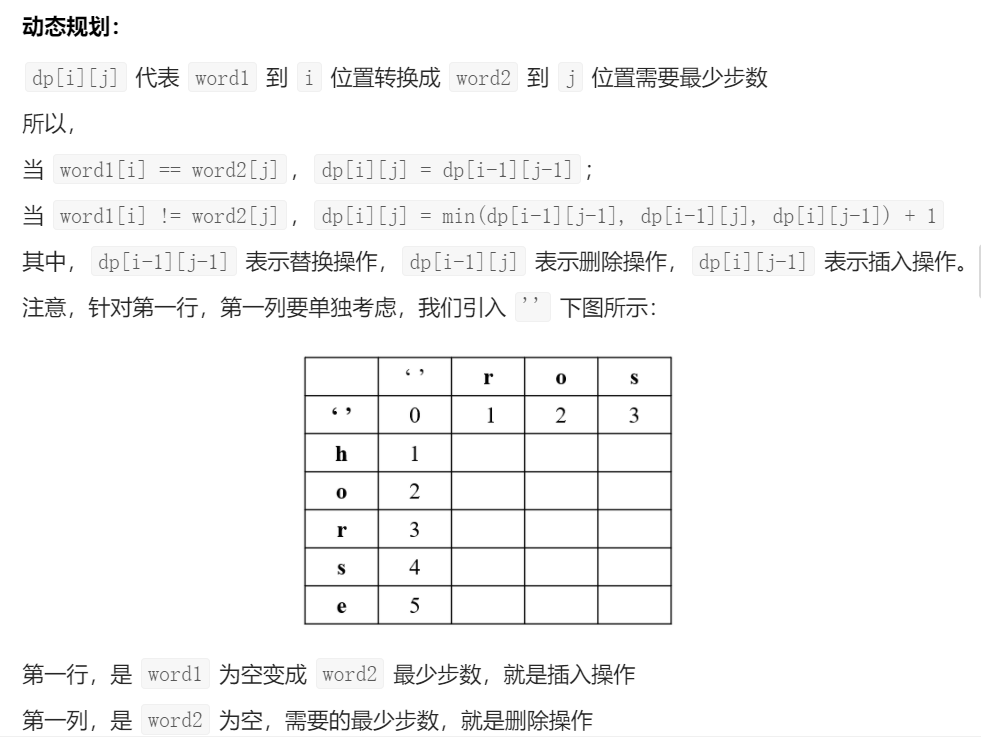
一定要考虑边界情况,二者均为空的情况,以及学习这种递推式的设计(到word1的i位置的字符串转为到word2的j位置的字符串这种关系的设计)
在i位置和j位置二者不一样时,对于替换删除和增加的理解:
因为是要把word1到i位置的字符串变成word2的字符串的j位置的字符串,所以最终的结果i位置和j位置一定是一样的。如果是替换,就相当于直接让二者的最后一个位置相等了,然后回过头来看dp[i-1][j-1]
如果是删除,那把word1的第i个删除掉,也只能回过头来看dp[i-1][j]了,如果是插入一个,那相当于i+1的位置和j的位置要一致,那就要回过头来看dp[i][j-1]了。所以有这三种递推式。千万记得这三种的选择都是一种操作,选出来最小的操作一定要加1.
DP就是有这种强大的能力让复杂事情简单化!
class Solution { public: int minDistance(string word1, string word2) { int m=word1.size(); int n=word2.size(); vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0)); //多一行一列存边界情况 for (int i = 0; i < m+1; i++) { dp[i][0] = i; } for (int j = 0; j < n+1; j++) { dp[0][j] = j; } for (int i = 1; i < m+1; i++) { for (int j = 1; j < n+1; j++) { if (word1[i - 1] == word2[j - 1]) { dp[i][j] = dp[i - 1][j - 1]; } else{ dp[i][j] = min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i][j - 1])) + 1; } } } return dp[m][n]; } };
原文:https://www.cnblogs.com/libin123/p/14675275.html